3次関数とは3次式で表される関数のことで、3次関数のグラフには変曲点があります。つまり、曲線の「山」になっている部分と「谷」になっている部分の境目の点のことです。
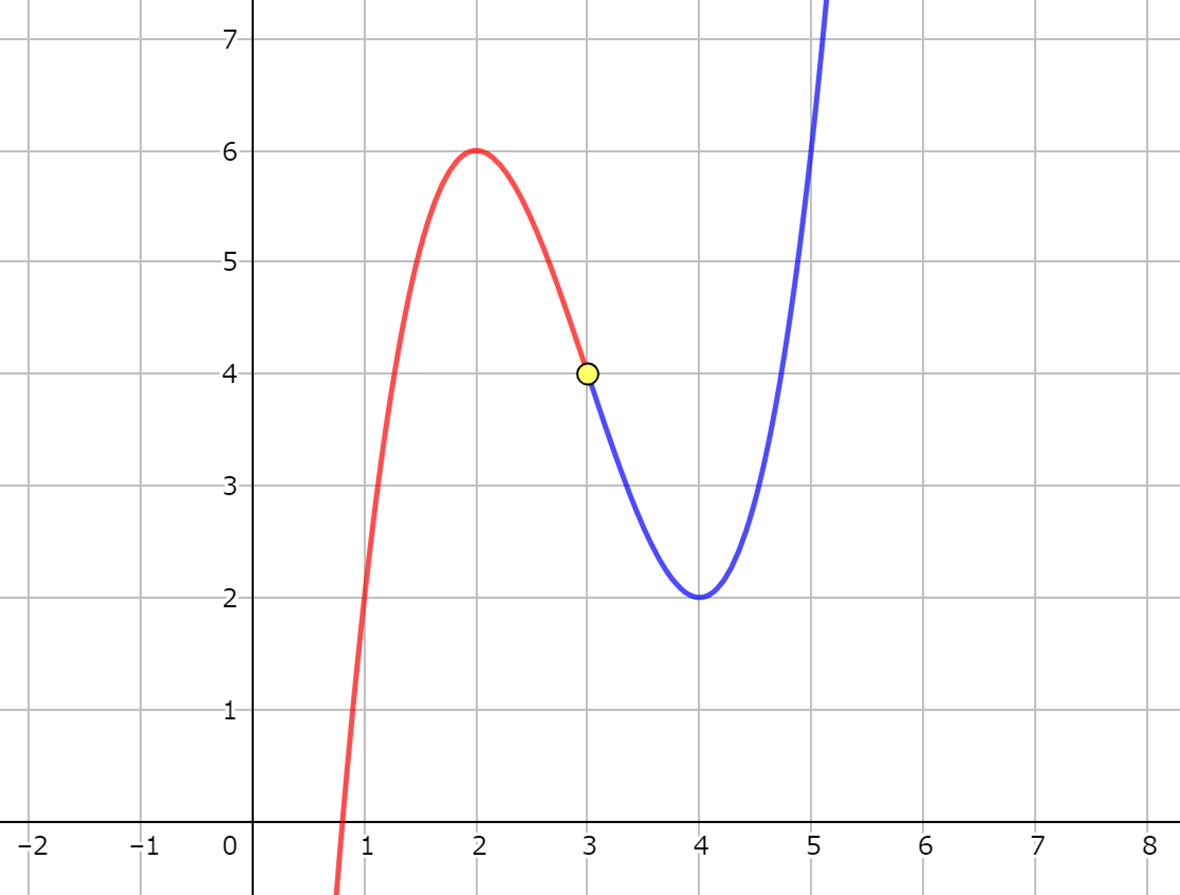
さらに、3次関数は変曲点に関して点対称という性質をもっています。
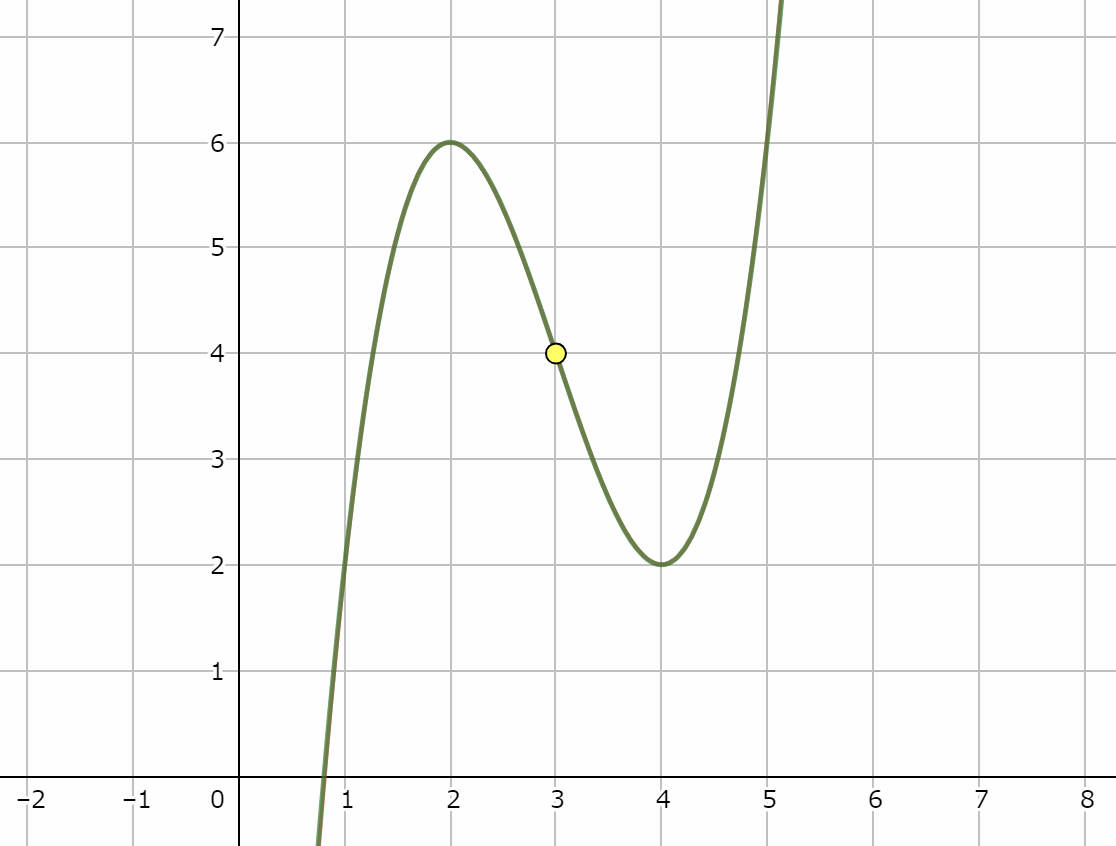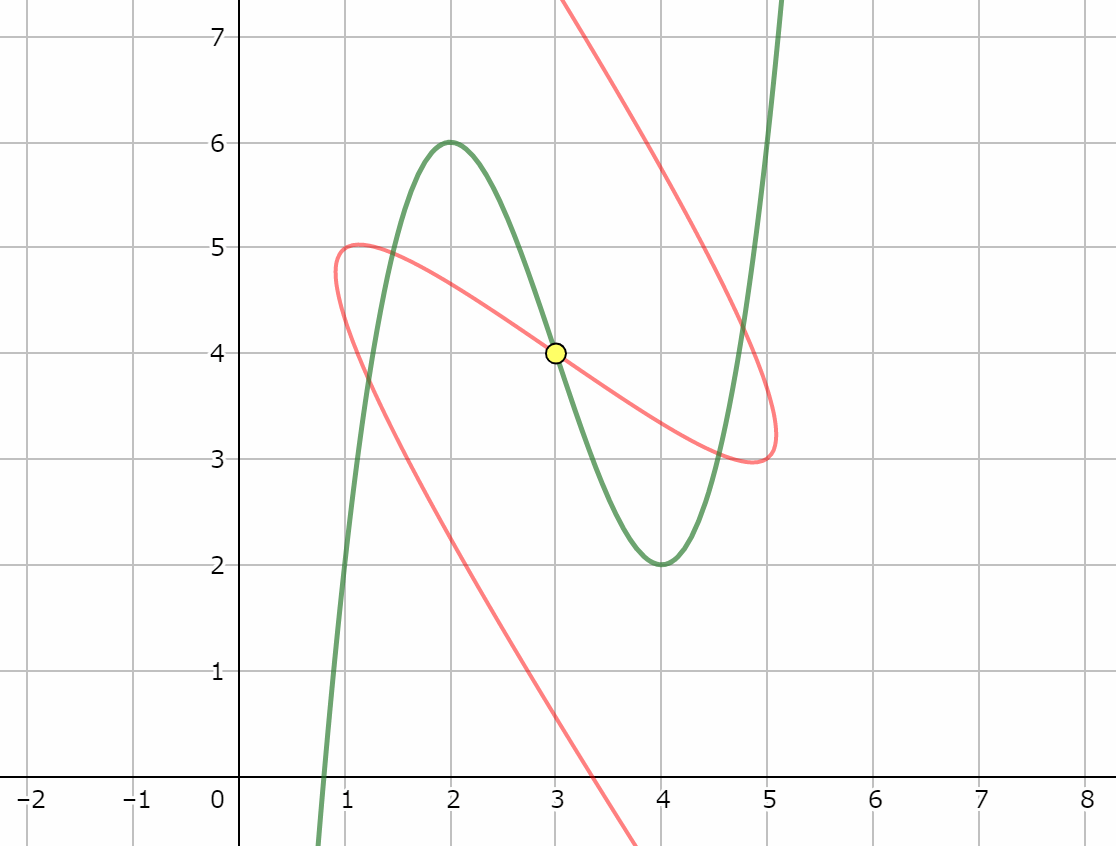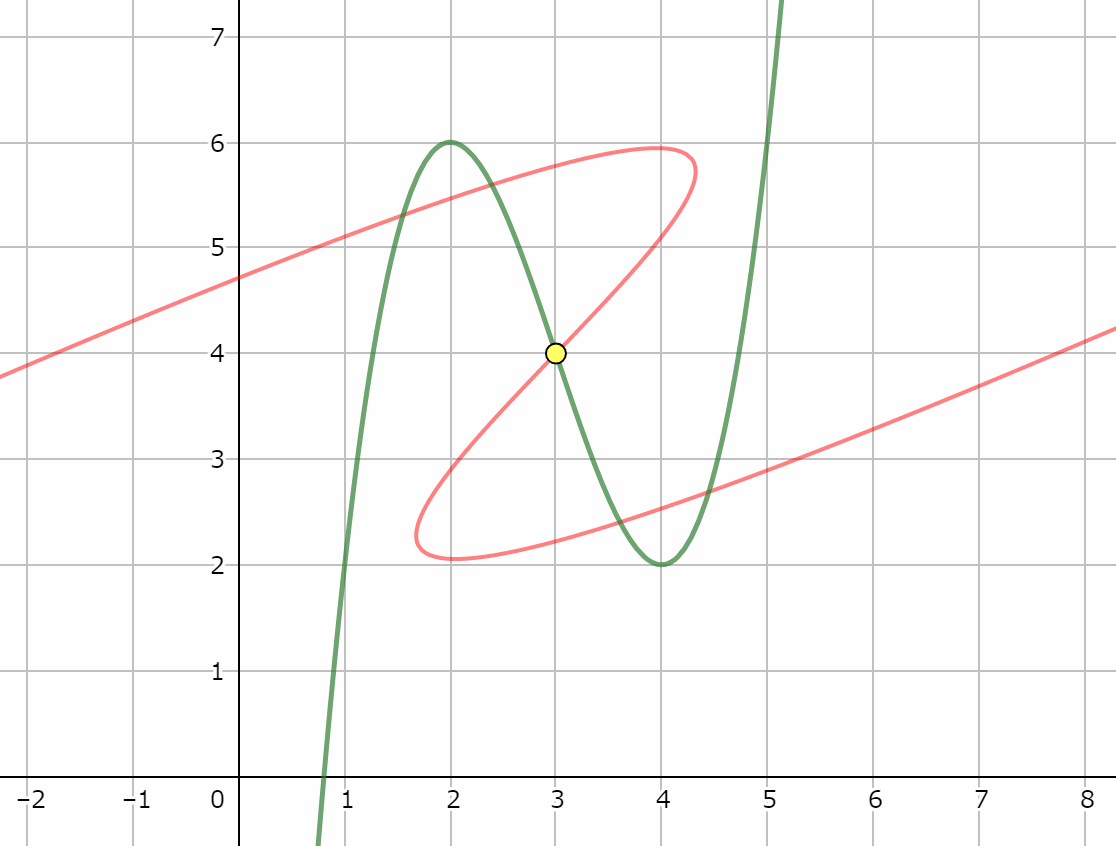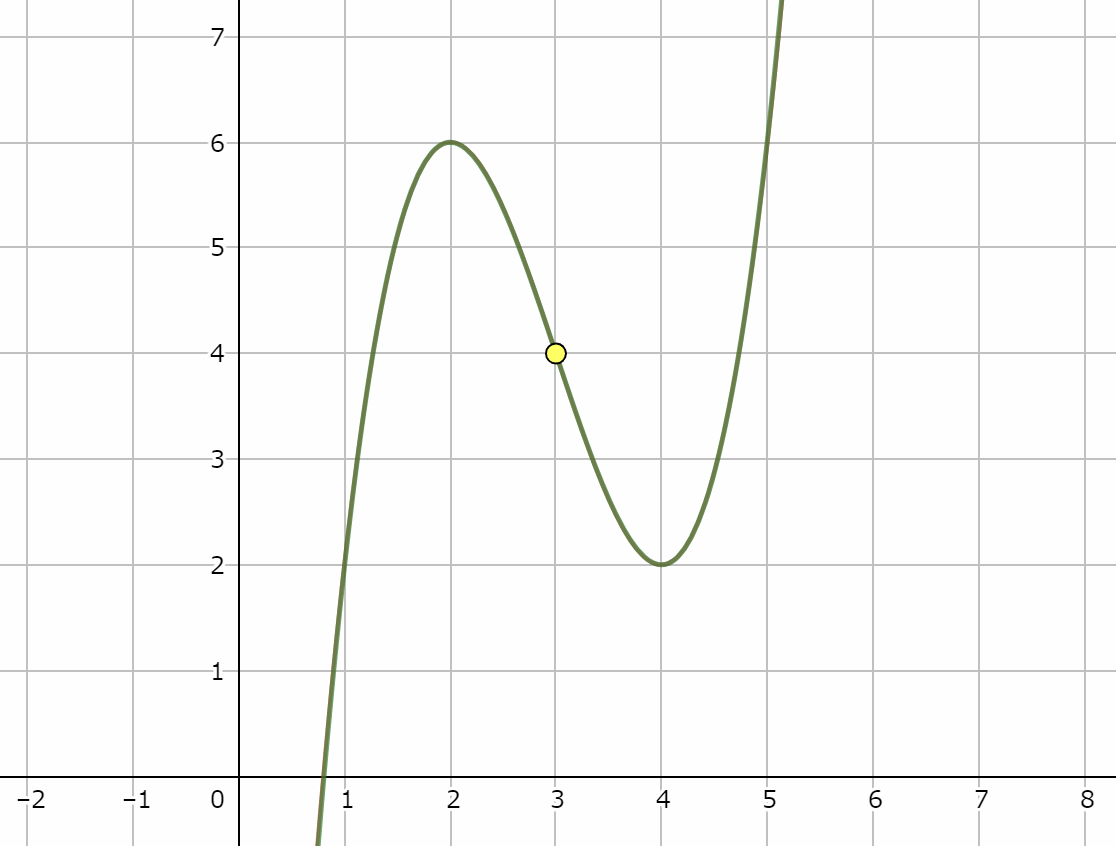
それではまた!
…ん?なんだこの手紙。

な、なんだってー!
盗まれた変曲点
うわあー!

何者かによって、3次関数のグラフの変曲点周辺を盗まれてしまいました。
しかも軸と
軸まで盗んでますね。
そして何より、パワポ初心者の怪盗にやられたのが悔しい。どうにかして見返したいところです。
…そうだ!
定規とコンパスを用いて変曲点を作図してやりましょう!
作図ルールの確認
3次関数のグラフが部分的に用意されているという特殊な状況のため、ルールの確認をしておきます。
まず、3次関数のグラフ上の点をとったり、3次関数と直線および円の交点をとることはOKとします。
しかし、以下の行為は禁止とします。
- 根拠なしに極値をとる点をとる
- 根拠なしに
軸や
軸に垂直な直線を引く
- 根拠なしに3次関数のグラフに接線(および接する円)を引く
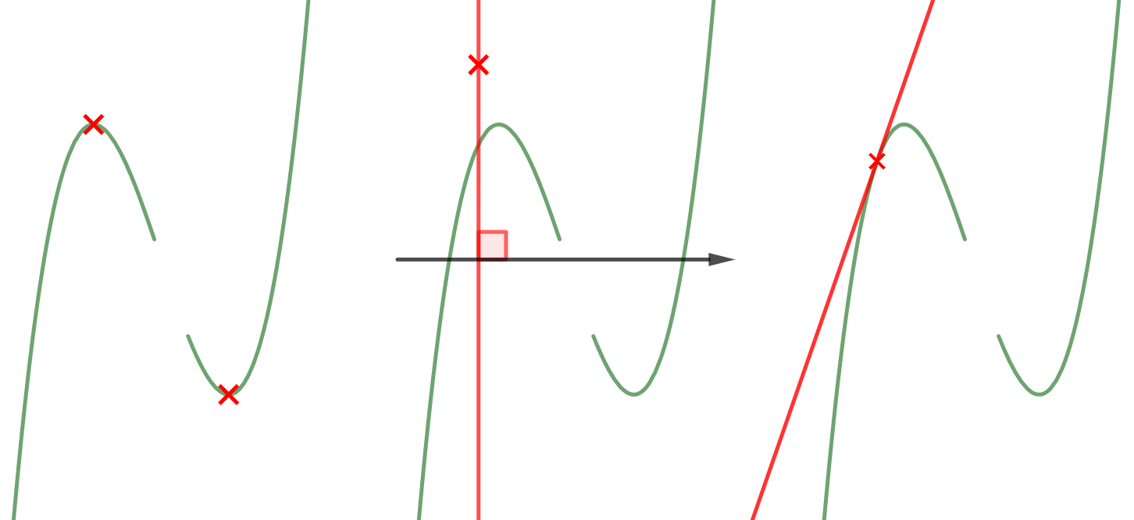
また、軸や
軸を盗まれているため、根拠なく
軸や
軸に垂直な直線を引くことも禁止します。接線や外接円についても(根拠なしに引くのは)禁止します。
以上のルールの下、3次関数の変曲点の作図を考えてみましょう。
…とは言うものの、何から手を付けたらいいのか分かりませんね。何より軸がないのが心細い。
闇雲に作図する前に、作図の方針でも考えますか。
作図の方針を決める
突然ですが、作図の前にちょっと計算をします。
3次関数をとおきます(上手く平行移動を施せば
の形にできるので、これを使っても大丈夫です)。このとき、
なので、変曲点の
座標
は
\[
x_0=-\frac{b}{3a}
\]となります。よって、座標が
となる点を2つ作図すれば、
軸に垂直で変曲点を通る直線が得られます。
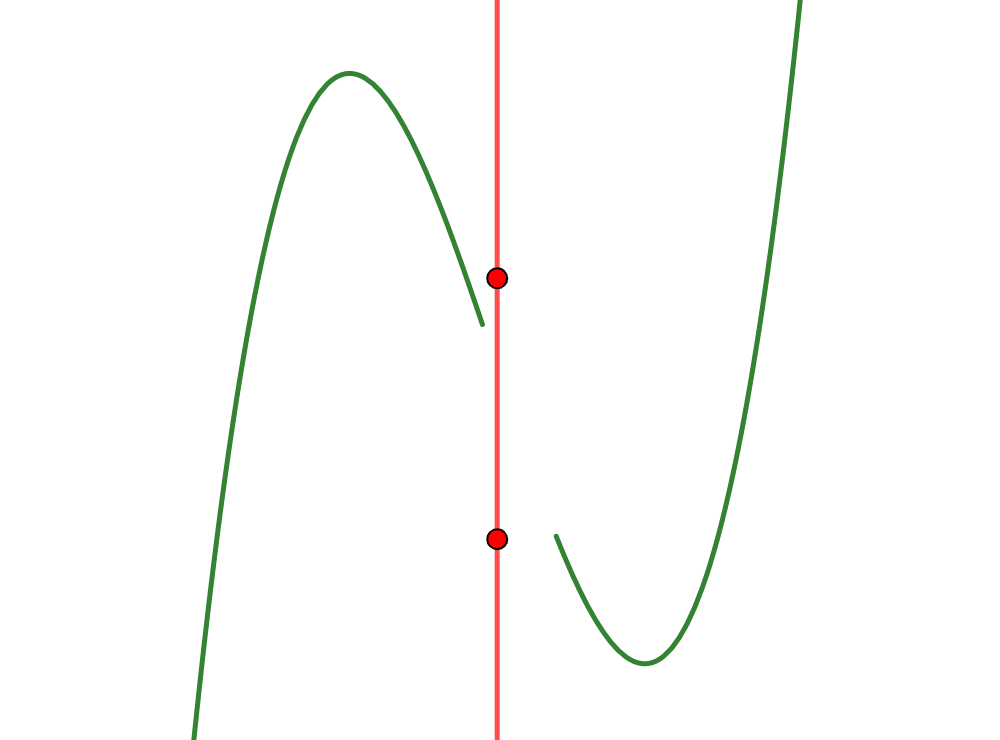
Step2は変曲点を通る直線をもう一本引くことです。
3次関数の点対称性を利用して、次の図のようにStep1で作った直線と等距離にある点を作図すればよさそうです。
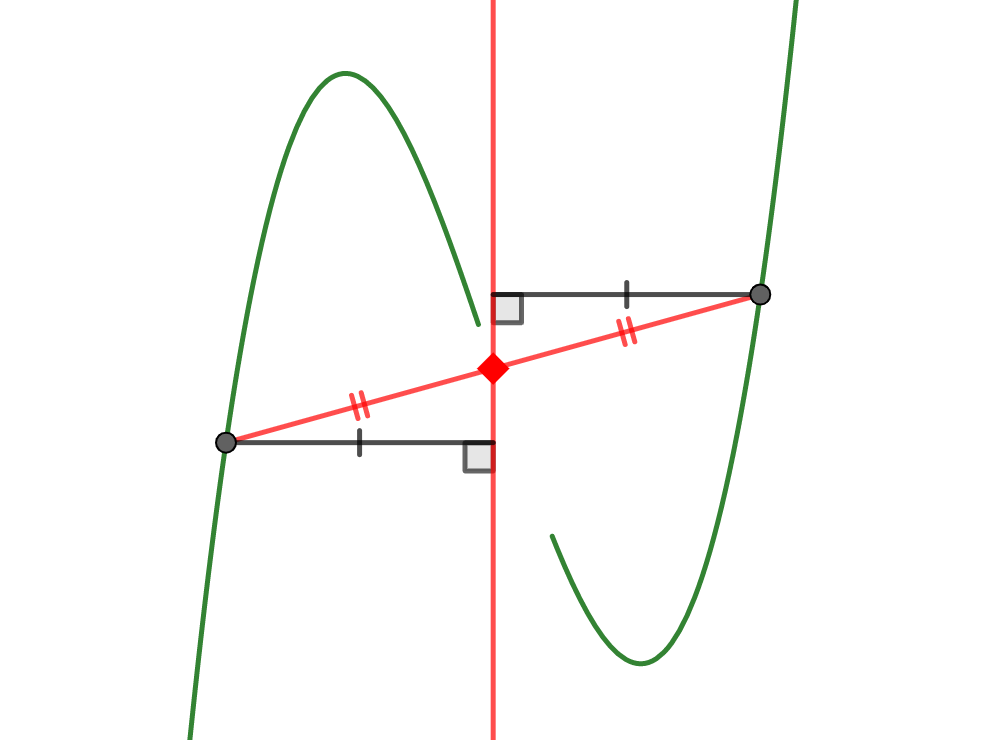
(以上をヒントに作図を考えてみたい方がいれば、ぜひここでスクロールを止めて考えてみてください!)
では、まずはStep1をがんばるぞー
…いや、ってどこよ。
直線と3次関数のグラフの交点
,
は私が勝手に与えた定数であり、そもそも原点の位置や1の大きさが分からないため、
の位置なんて分かりません。
このままずっと考えてるのもアレなんで、ひとまず交点が3つになるように直線を引いてみます。
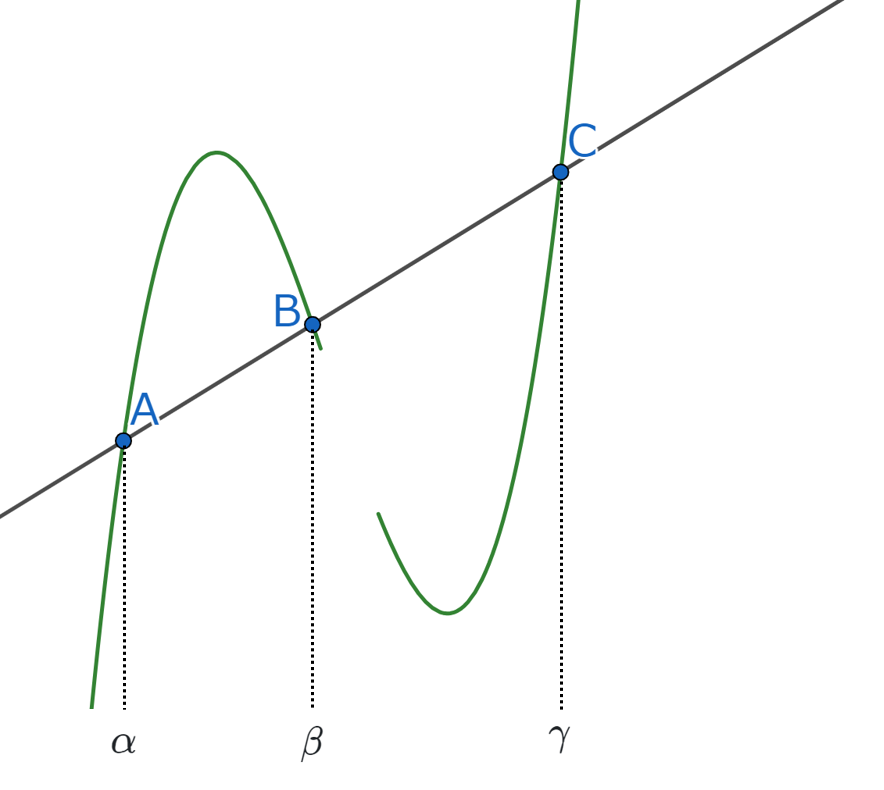
交点の座標を小さい順に
,
,
としました*1。
仮にその直線の方程式をとすると、
,
,
は
、つまり
\[
ax^3+bx^2+(c-s)x+d-t=0
\]の解になります。
ここで注目したいのは「と
の係数」です。直線の方程式は1次式なので、どんな直線を引いても2次以上の項の係数には影響を与えません。これは作図をする上で使えそうな値です。
すると、解と係数の関係により
\begin{align*}
&\alpha+\beta+\gamma=-\frac{b}{a}=3x_0\\
&x_0=\frac{\alpha+\beta+\gamma}{3}
\end{align*}となります。これはうまい!
これにより、座標が
,
,
の平均値となる点を作図をすればよいことになります。これなら作図ができそうですね!
変曲点の作図
それでは作図を始めていきましょう。
Step1の作図
まずは3次関数と3点で交わるように直線を引きます。
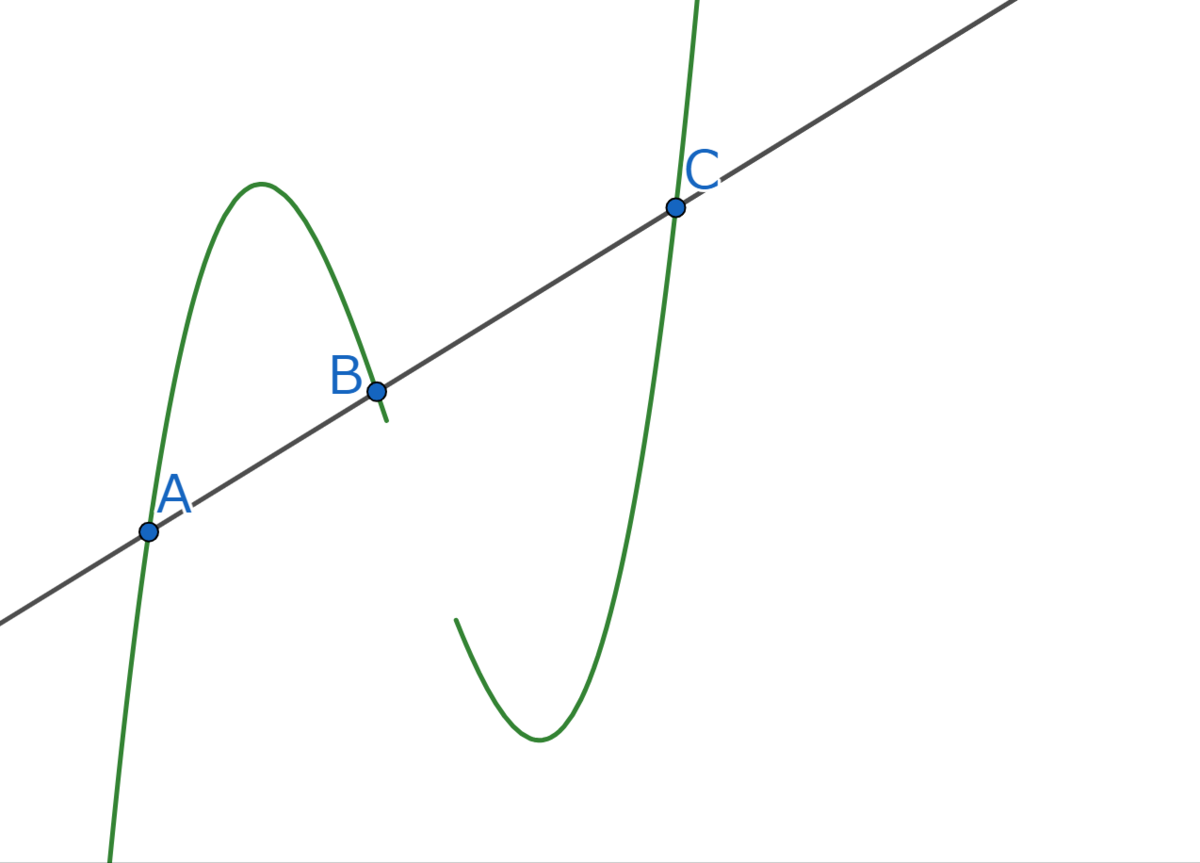
次に、コンパスでの長さを測り、図のように
となる点を作図します。
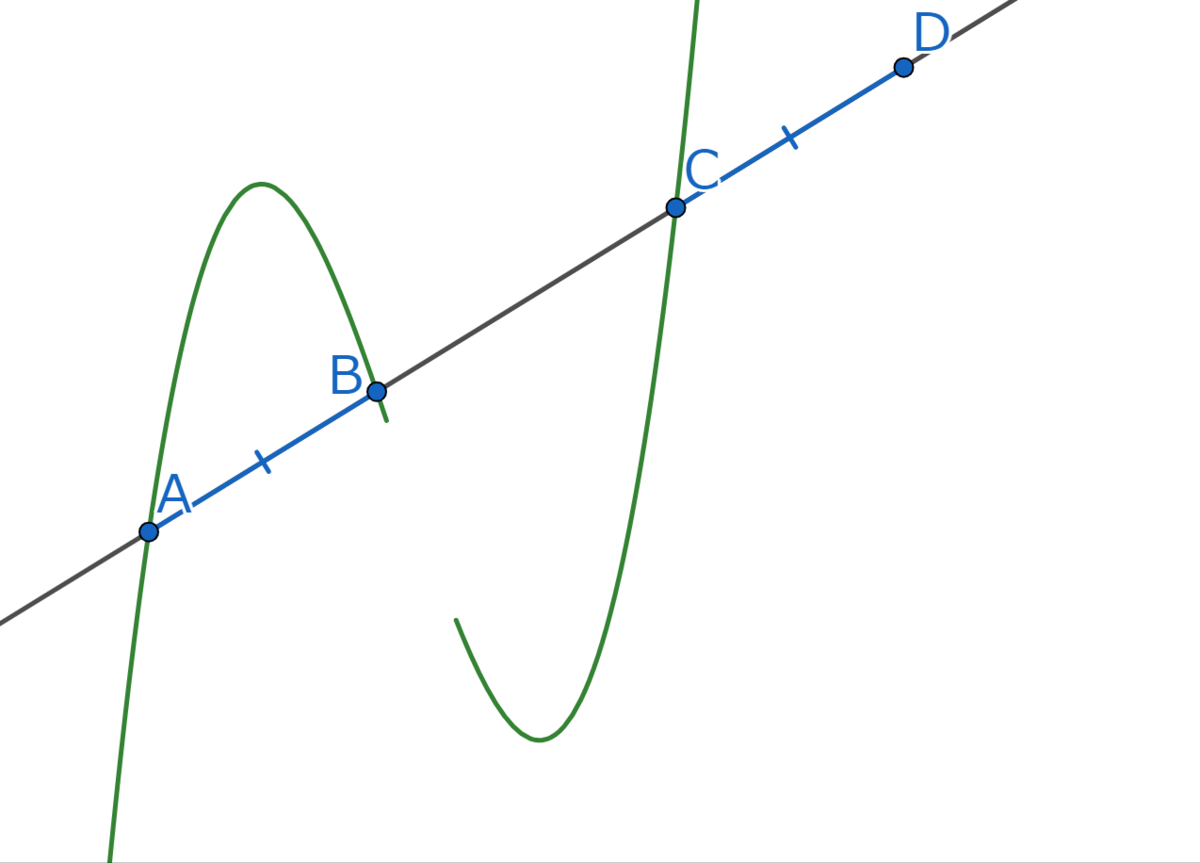
ここで、の長さを(Aを基準として)1/3倍にした点こそがStep1で作図したい点になります。よって、線分
を
に内分する点を作図します。
まず適当に点をとって直線
を引きます。
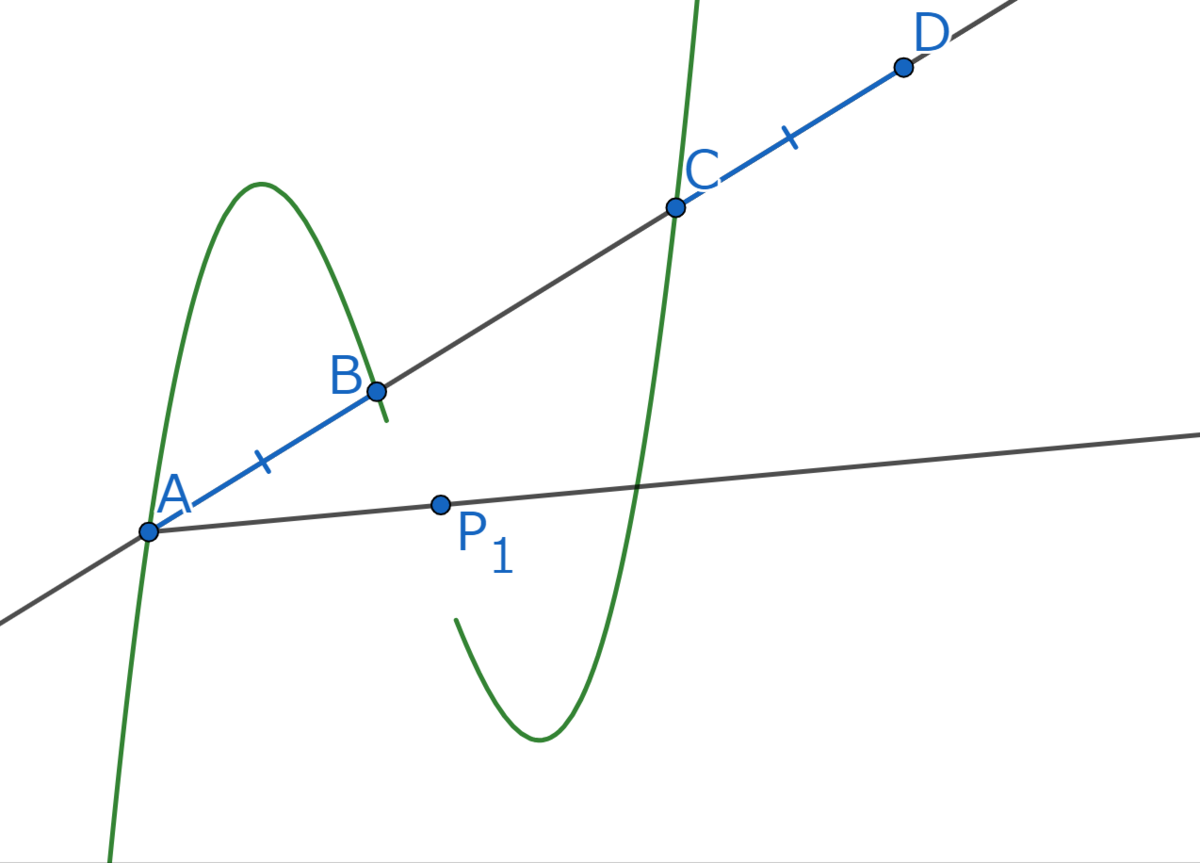
線分の長さをコンパスで測り、ピッピッとやって
,
を作図します。
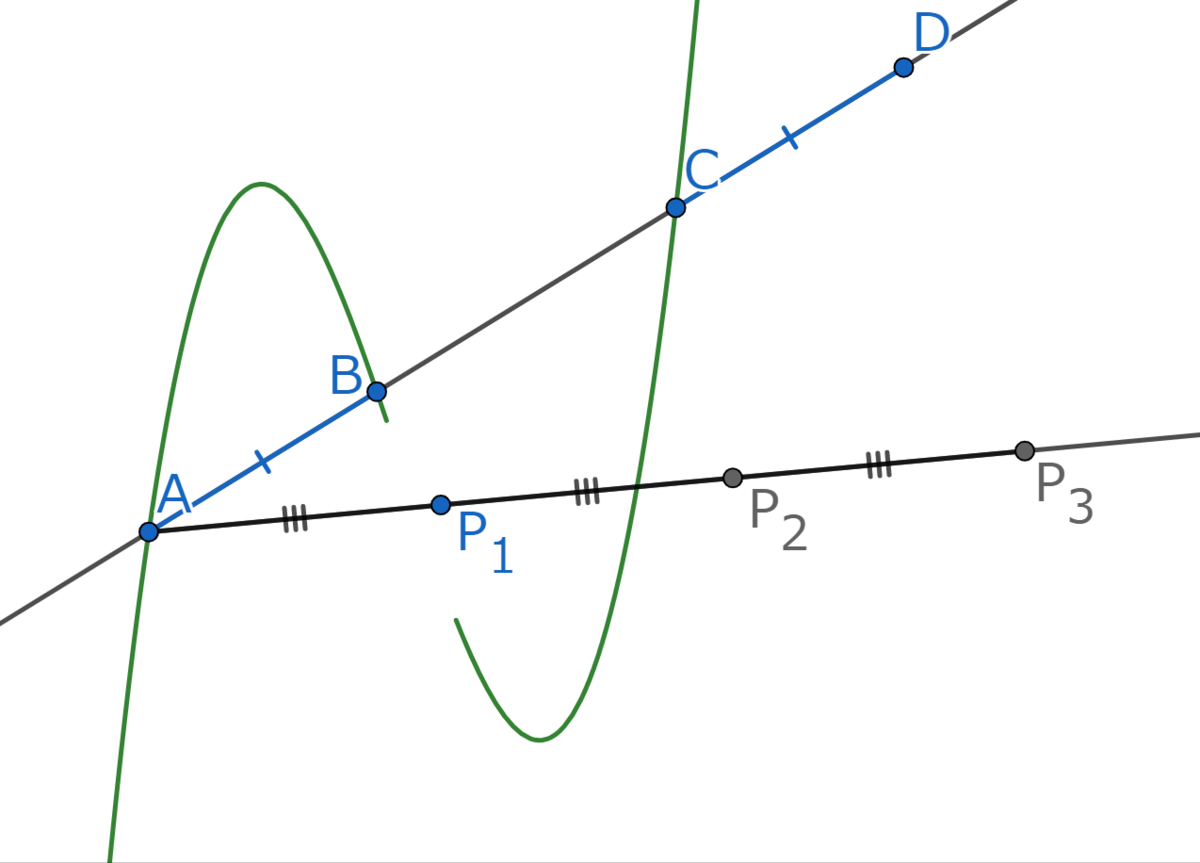
直線を引き、これに平行で
を通る直線を引き、
との交点を
とおきます(平行線の作図の跡は省略しました)。
点は線分
を
に内分する点で、
座標は変曲点の
座標と同じです!
\[
\frac{\beta'+\gamma'}{3}+\alpha=\frac{\alpha+\beta+\gamma}{3}
\]となります。
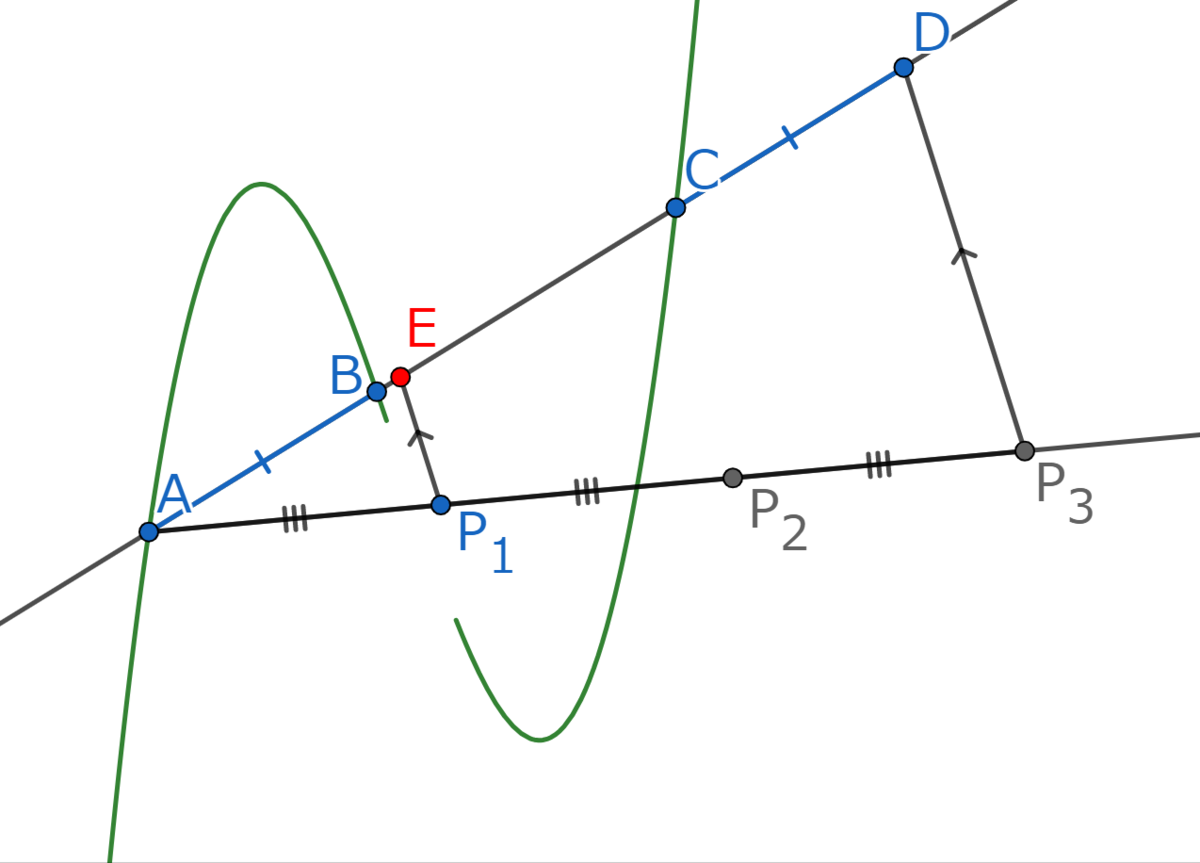
そして、再度3次関数との交点が3つになるような直線を引き直して、同じ手順で「座標が変曲点と同じ点」を作図します。
最後に直線を引いて、Step1は終了です。
Step2の作図
いよいよ大詰めです。方針を決めるセクションでも言った通り、3次関数のグラフの点対称性を利用します。
まず、以下のようにとなる点
をとります。
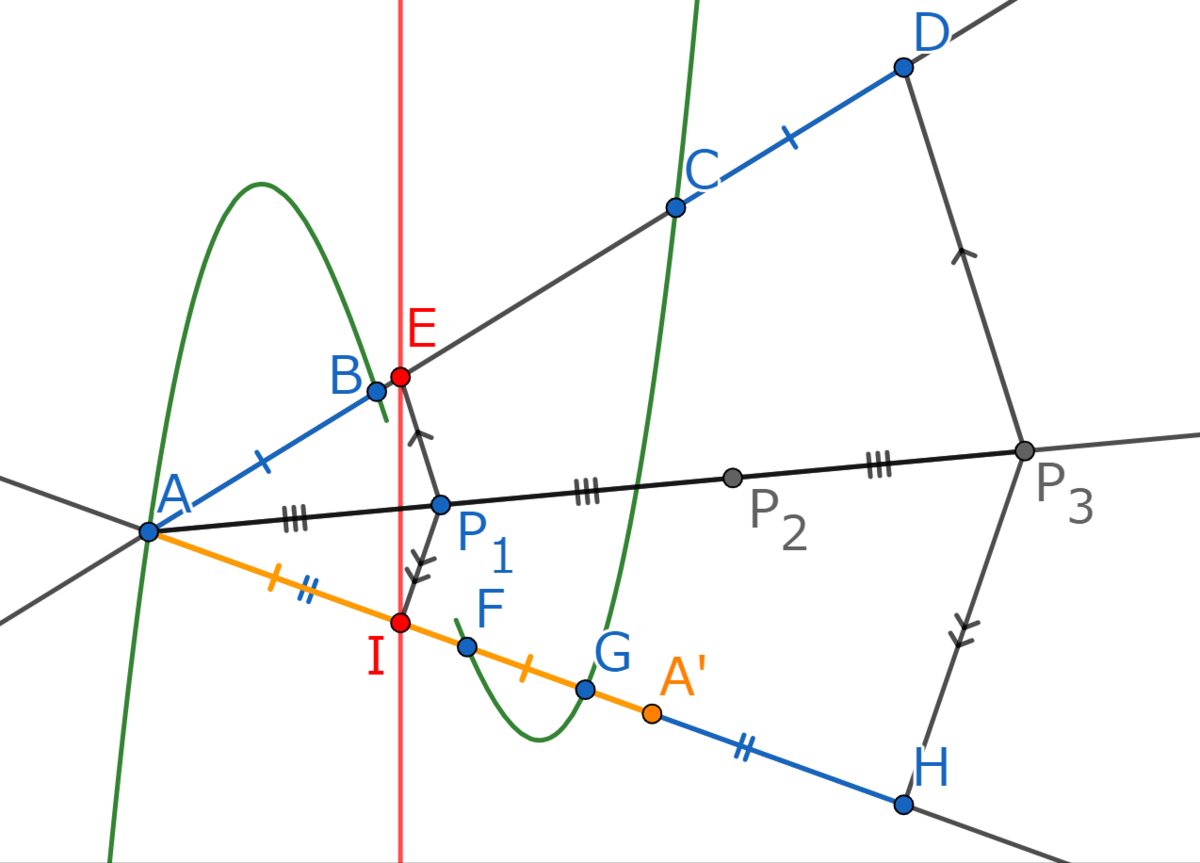
次に点を通り、Step1で得た直線と平行な直線を引き、3次関数との交点を
とおきます。
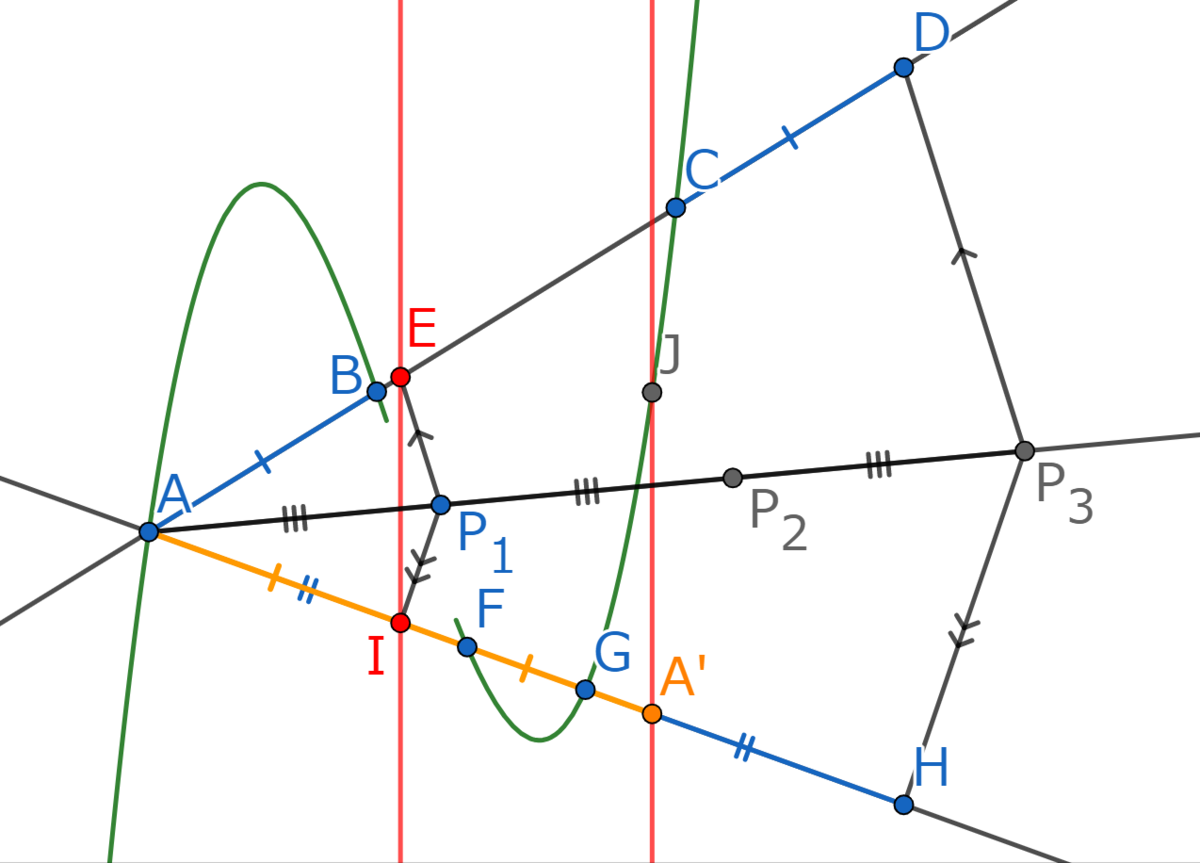
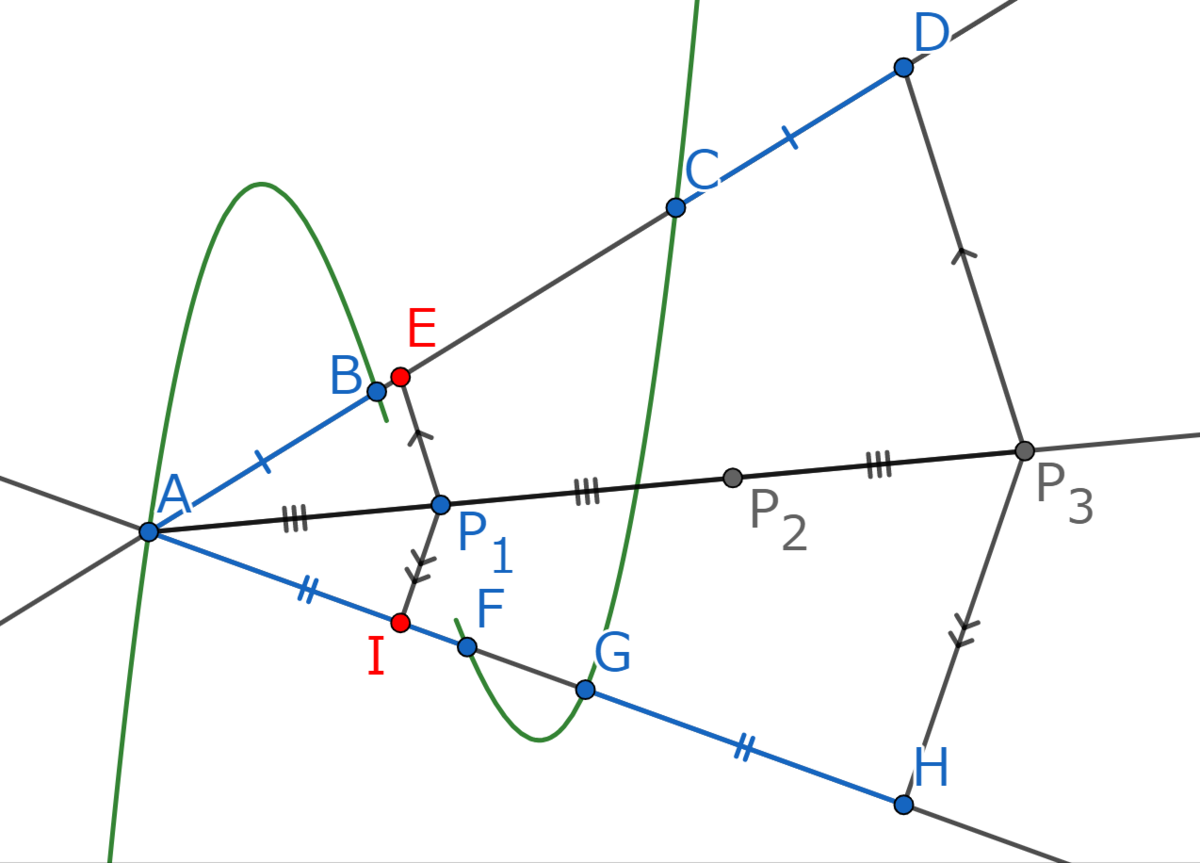
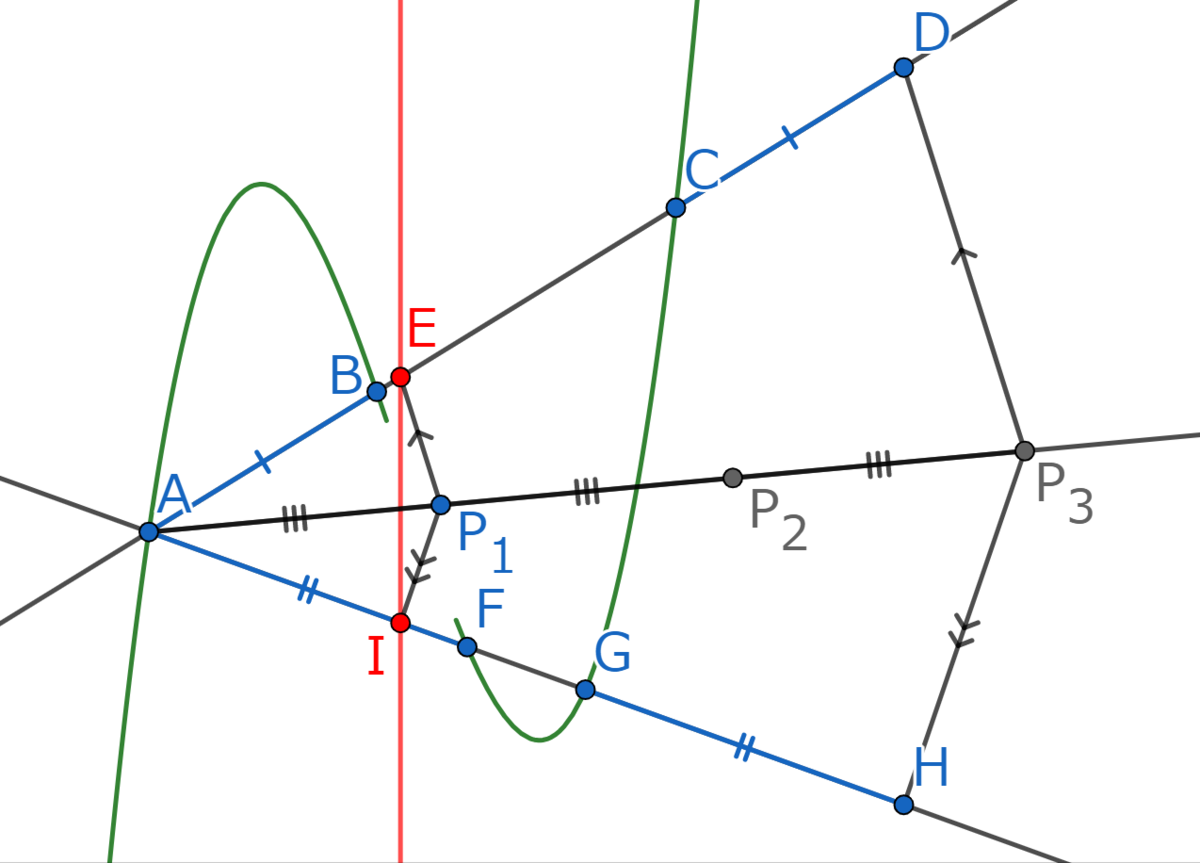
そして、点と点
を結べば…!
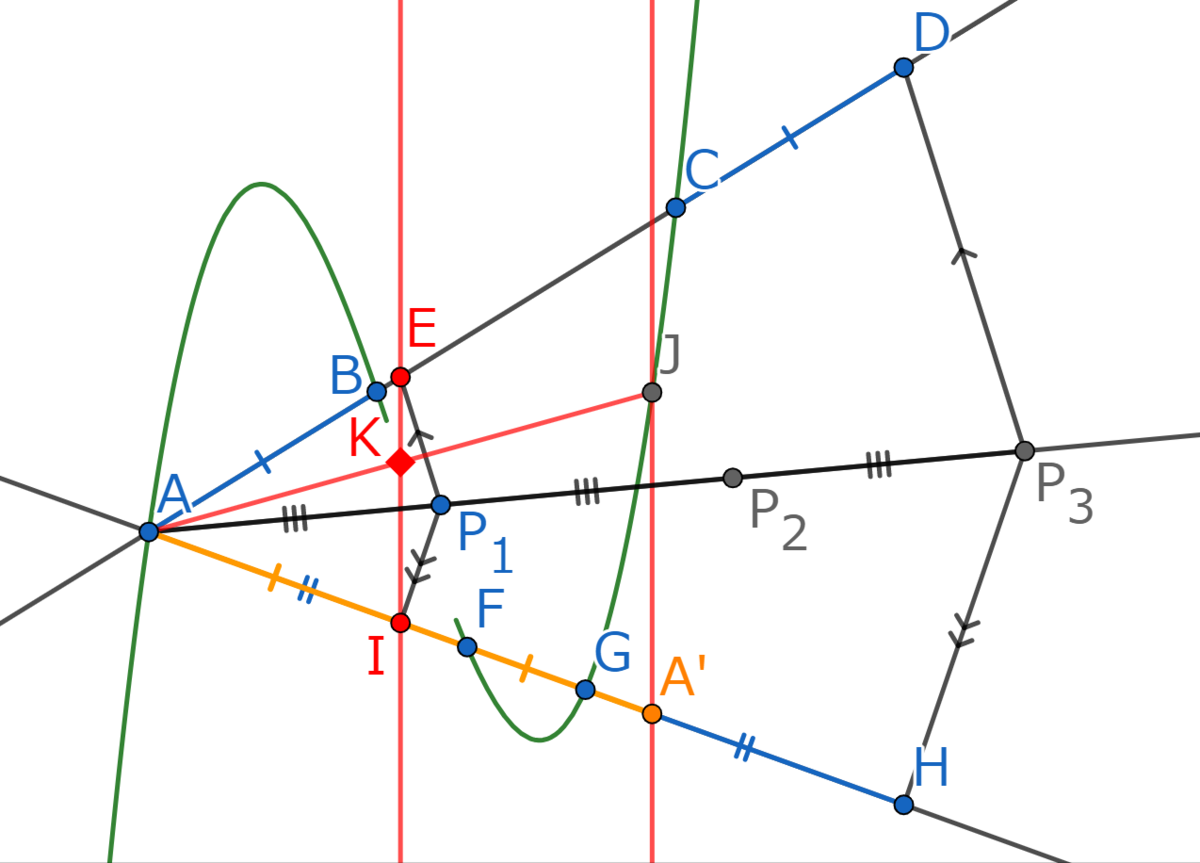
点と点
は3次関数のグラフ上の点で、直線
を挟んで互いに反対側にあり、
をみたします。
よって点は変曲点です!
まとめ
次の3次関数の性質を用いて、変曲点の作図をしてみました:
- 3次関数は変曲点に関して点対称である
- 3点で交わるように直線を引いたとき、(変曲点の
座標)=(交点の
座標の平均値)
特に、(2)の性質は解と係数の関係によって導出できるというのが面白ポイントでしたね。
これでもう、変曲点怪盗が現れても大丈夫でしょう。
怪盗め!パワポ勉強して おとといきやがれ!
thank Q for rEaDing.φ(・▽・ )
補足(怪盗の反省)
(以後、私の一連の作業をこっそり見ていた怪盗の反省です。)
おのれ。せっかく変曲点を手に入れたのに、作図で復元されてしまった。一体どうすればよかったのか、反省をするのだ!
いや、反省の前に、ヤツが持っていた3次関数に何か細工がされていた可能性がある。極値をとらないだったら、作図できなかったのではなかろうか?少し考えてみるのだ。
…ぐぬぬ、同じ手順で変曲点の作図ができてしまった。
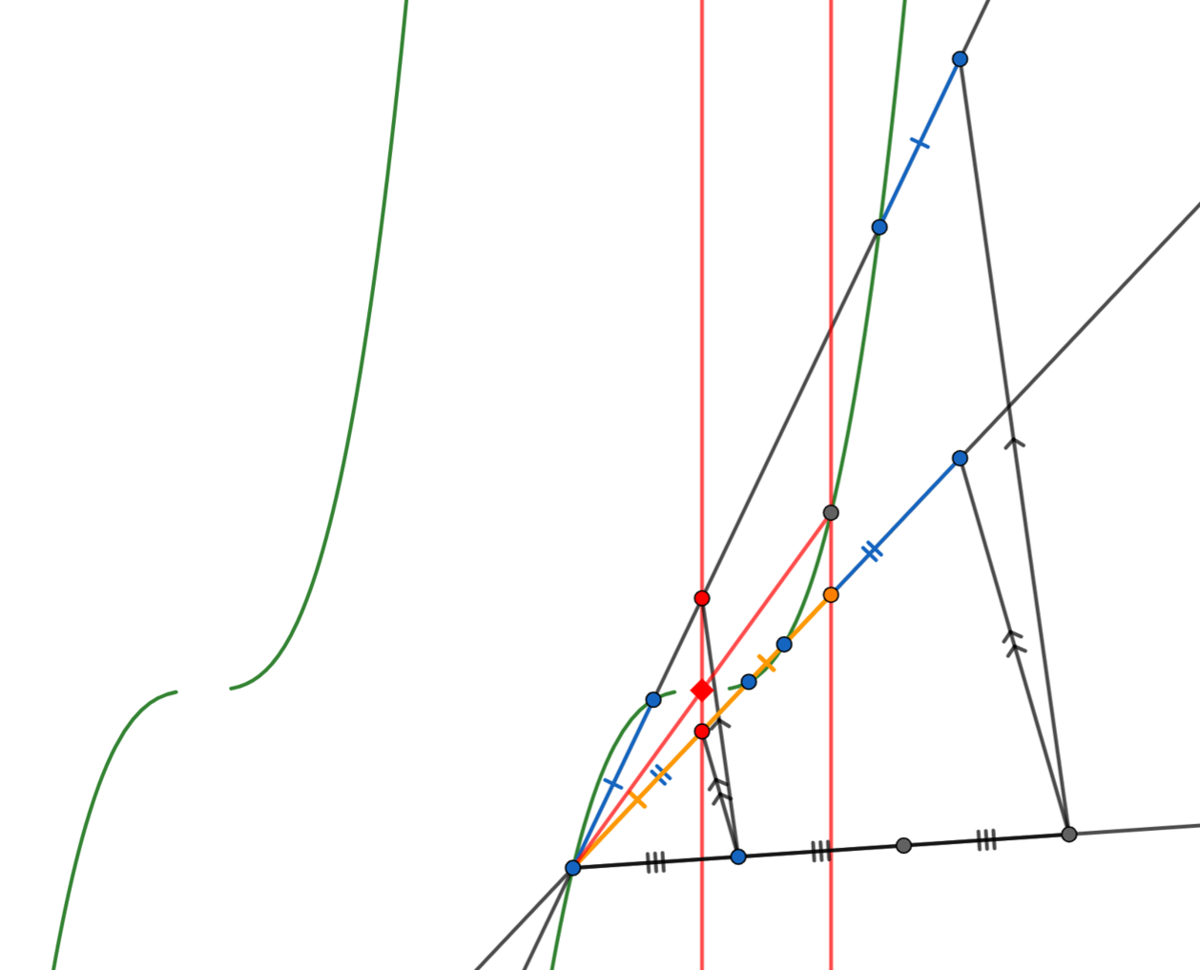
どうやら3次関数の形状には依存しないようだ。小癪な。
ところで、ヤツの作図を振り返ると、最初に3次関数と交点が3つ取れるように直線を引いていたようだな。つまり、3次関数と3点で交わるように直線が引けることが前提になっていることがわかる。
よし!この前提を崩すのだ!
(怪盗 長考中)
ぐぬぬ、少し考えてみたのだが、極値をとる点まで盗んだとしても、図のようにグラフ上の2点をとって直線を引けば、反対側で1点と交わるようだ。
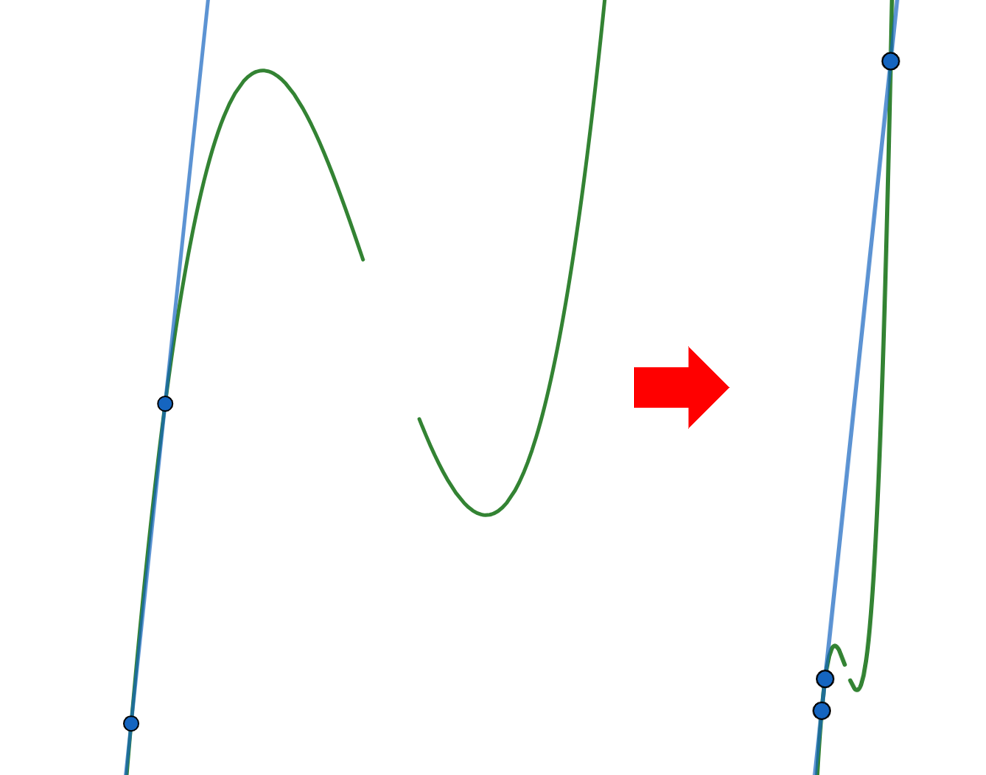
つまり、盗む範囲が有界であれば変曲点は作図可能だとわかるな!?
では、盗む範囲が非有界の場合で、3点で交点をもつように直線が引けない例がないだろうか。
(怪盗 長考中)
おお、ついに見つけたぞ!
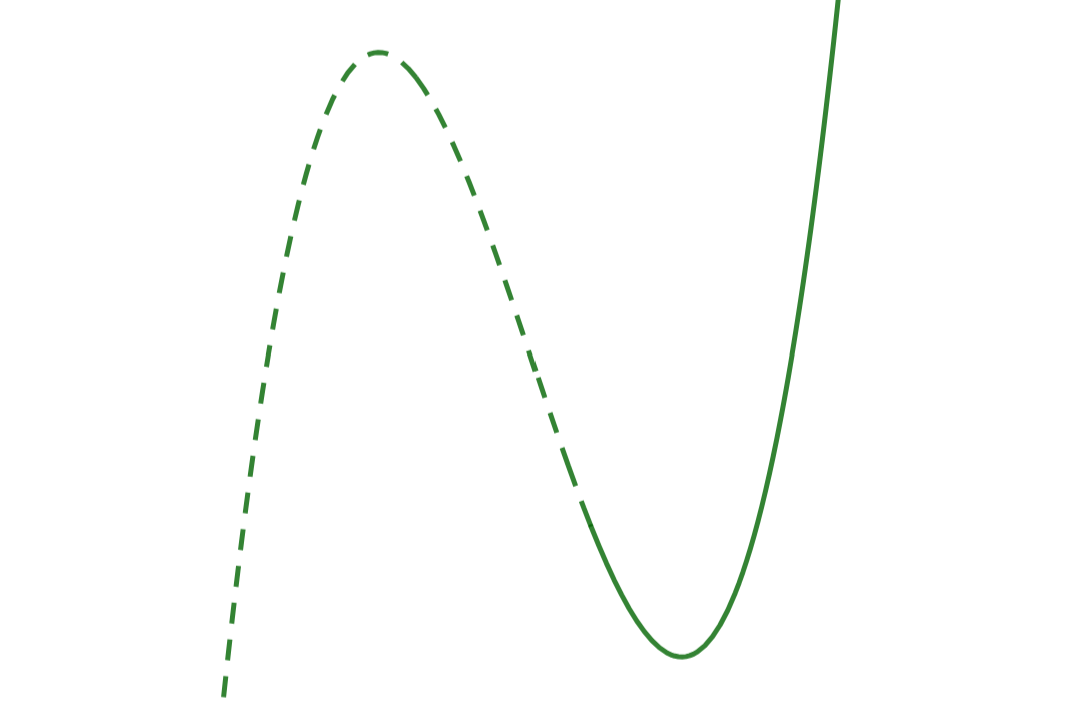
この点線部分をすべて奪えば、3点で交点をもつように直線が引けないな!?不安ならグラフをすべて奪えばよかろう。
ふははは、今に見てろコロちゃんぬ。この屈辱は必ず返す!
To Be Continued...?
*1:交点から真下に下した点線は、現時点では作図によって得られません。