$F_0=0$,$F_1=1$,$F_{n+2}=F_{n+1}+F_n\; (n=0,1,2,\ldots)$をみたす数列$(F_n)_n$をフィボナッチ数列と言います。1つ前の数と2つ前の数を足してできる数列で、具体的には
\begin{align*}
F_0&=0,\\
F_1&=1,\\
F_2&=1+0=1,\\
F_3&=1+1=2,\\
F_4&=2+1=3,\\
F_5&=3+2=5,\\
F_6&=5+3=8,\\
F_7&=8+5=13,\\
F_8&=13+8=21,\\
F_9&=21+13=34,\\
F_{10}&=34+21=55
\end{align*}のように変化していく数列になっております。
いきなりですが、フィボナッチ数列の一般項は
\[
F_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)
\]で表されることが知られています。こう見えてもすべて自然数というだけでも面白いですね。この公式は高校生のときに計算して知ったのですが、思ったよりも複雑で驚いたのを覚えています。
本日はこのフィボナッチ数列の一般項を斉次2階線形微分方程式に帰着させて求めようと思います。
なお、次の定義および定理は既知とします。
\[
e^x = \sum_{n=0}^{\infty}\frac{1}{n!}x^{n}=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots
\]で与えられる.
\begin{equation}y''(x)+p(x)y'(x)+q(x)y(x)=0\quad(\forall x\in I)\label{1}
\end{equation}
冪級数の導入と収束性・微分可能性
いきなりですが、次のような冪級数を導入します。
\begin{align*}
f(x)&=\sum_{n=0}^{\infty}\frac{F_n}{n!}x^n\\
&=\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{2}{3!}x^3+\frac{3}{4!}x^4+\frac{5}{5!}x^5+\cdots
\end{align*}
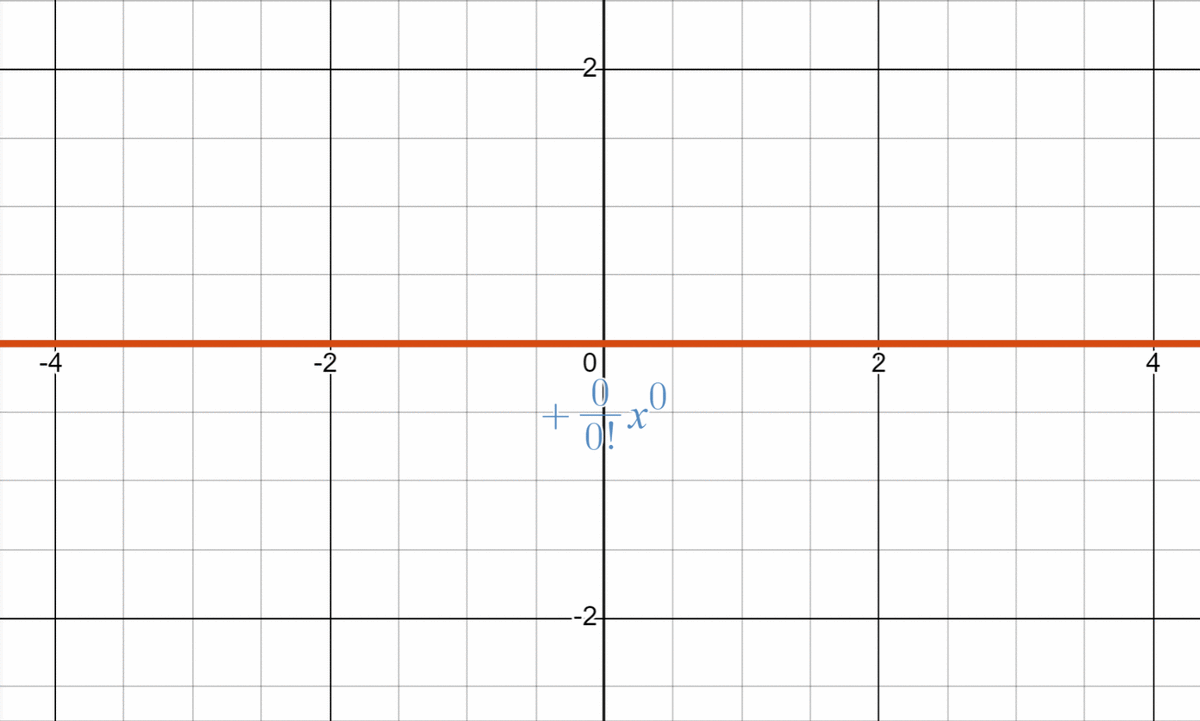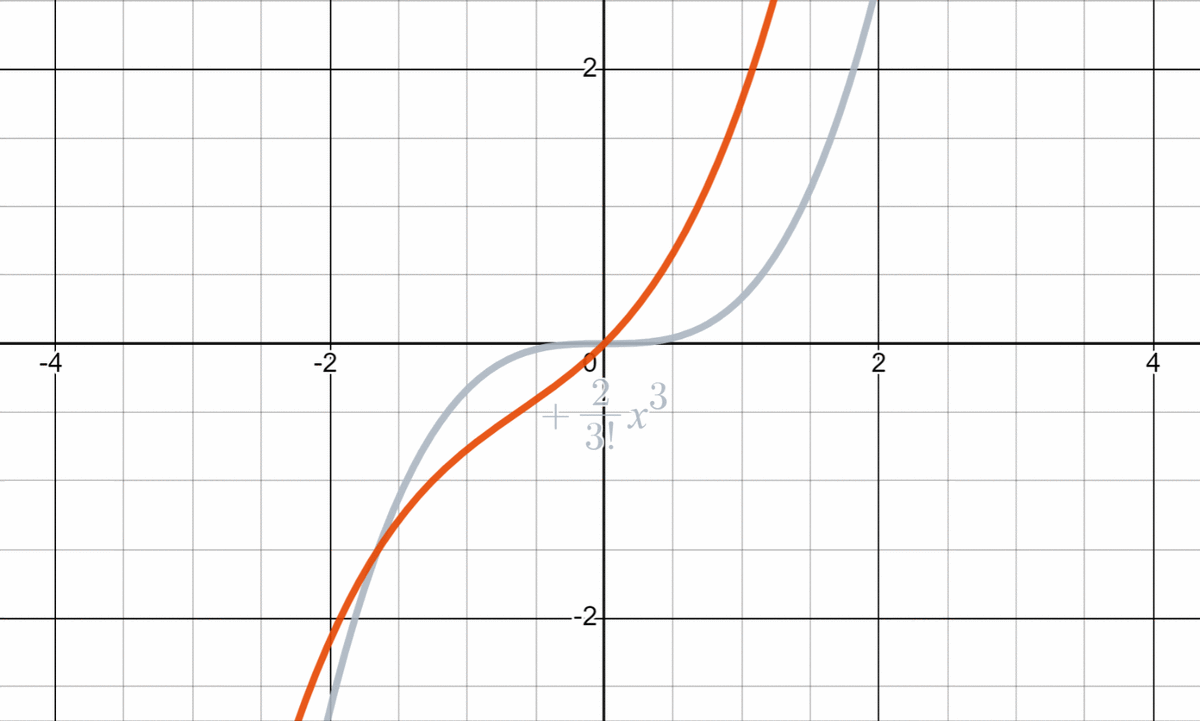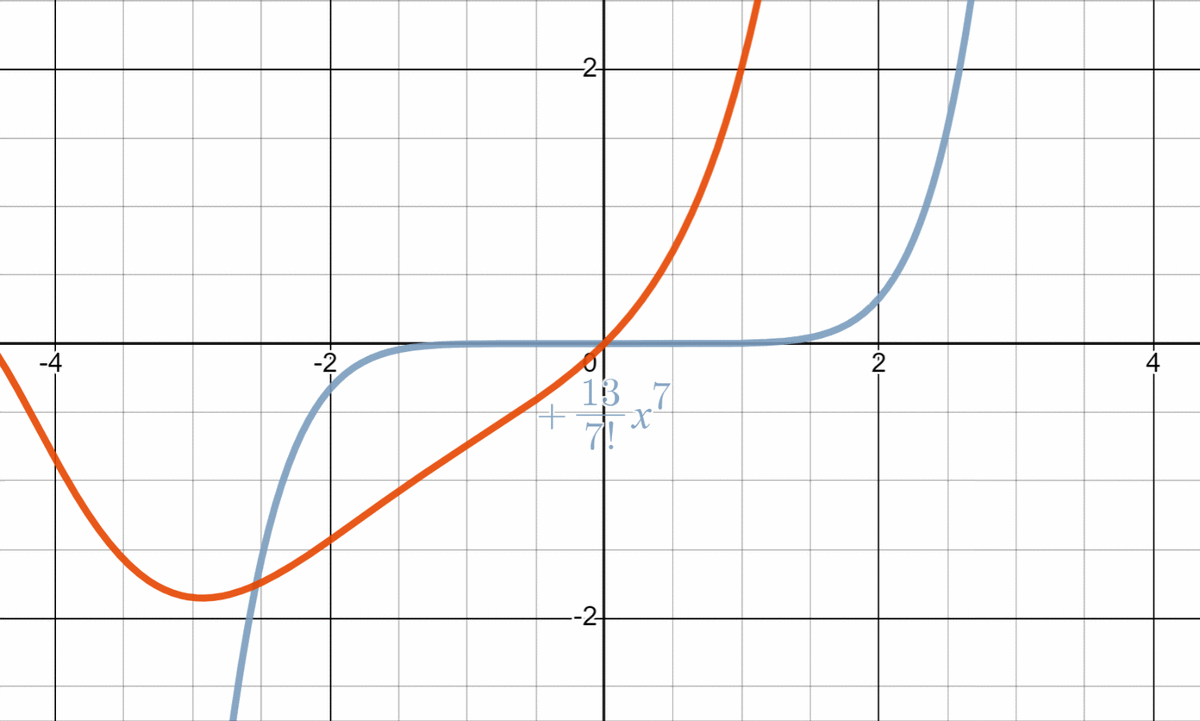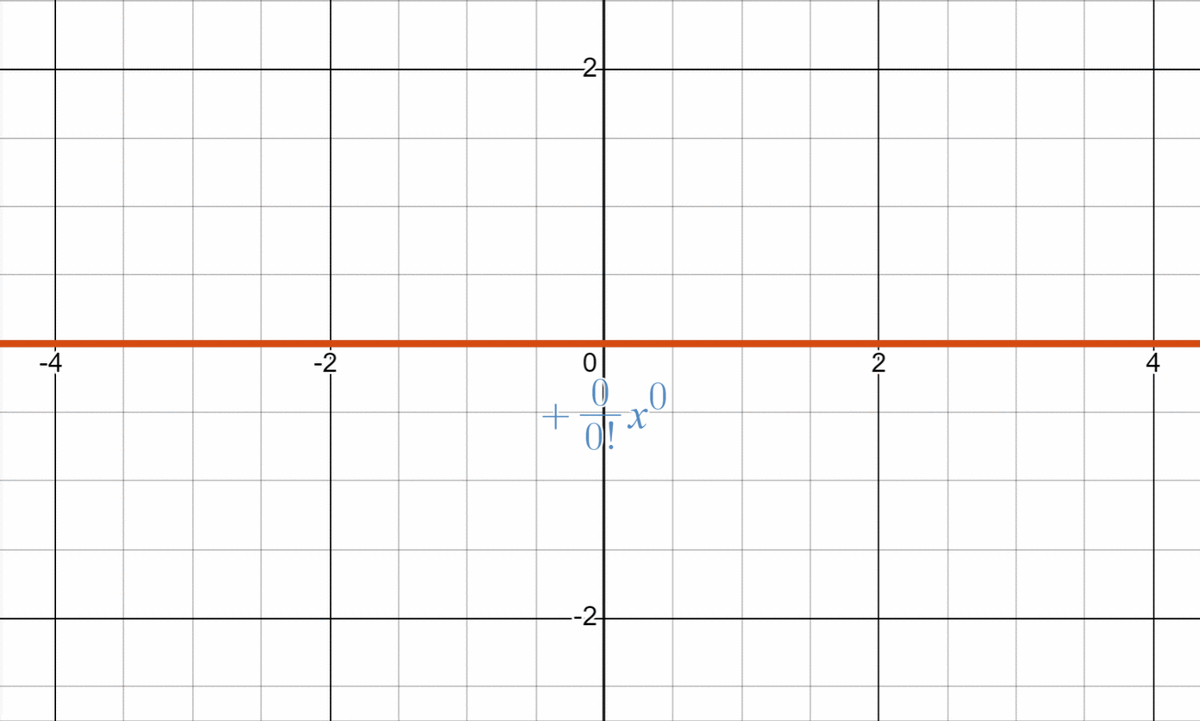
実際、この冪級数の収束半径を調べると
\begin{align*}
\left| \frac{F_{n+1}}{(n+1)!}\div\frac{F_n}{n!}\right|
&=\frac{F_{n+1}}{nF_n}\\
&=\frac{F_n + F_{n-1}}{nF_n}\\
&\le\frac{F_n + F_n}{nF_n}\\
&=\frac{2}{n}\\
&\longrightarrow 0\quad(n\to\infty)
\end{align*}となるため、収束半径は$\infty$となります。また、冪級数の微分は項別に微分すればよいので、$f(x)=\sum\limits_{n=0}^{\infty}\frac{F_n}{n!}x^n$の微分は\begin{align*}
f'(x)&=\sum_{n=1}^{\infty}\frac{nF_n}{n!}x^{n-1}\\
&=\sum_{n=1}^{\infty}\frac{F_n}{(n-1)!}x^{n-1}\\
&=\sum_{n=0}^{\infty}\frac{F_{n+1}}{n!}x^n
\end{align*}となります。ついでにもう一度微分すると
\[
f''(x)=\sum_{n=0}^{\infty}\frac{F_{n+2}}{n!}x^n
\]となります。
つまり、$\sum\limits_{n=0}^{\infty}\frac{a_n}{n!}x^n$という形の級数の微分は、数列を1つずらせばよいことが分かります。
2階線形微分方程式に帰着
ところで、フィボナッチ数列は$F_{n+2}=F_{n+1}+F_n\; (n=0,1,2,\ldots)$をみたす数列でした。$f''$をよく見ると
\begin{align*}
f''(x)
&=\sum_{n=0}^{\infty}\frac{F_{n+2}}{n!}x^n\\
&=\sum_{n=0}^{\infty}\frac{F_{n+1}+F_n}{n!}x^n\\
&=\sum_{n=0}^{\infty}\frac{F_{n+1}}{n!}x^n+\sum_{n=0}^{\infty}\frac{F_n}{n!}x^n\\
&=f'(x)+f(x)
\end{align*}となること、すなわち$f$は2階線形微分方程式
\begin{equation}
y''(x)-y'(x)-y(x)=0\label{2}
\end{equation}をみたすことが分かります!
より詳しく言うと、定数係数かつ定数項が$0$のため、定数係数の斉次2階線形微分方程式となっています(スタバの注文かよ)。
斉次2階線形微分方程式は、基本解を見つければ一般解を表示できることが知られていますが、定数係数の場合は基本解を簡単に求められます。
まず、$y(x)=e^{\lambda x}$とおいて\eqref{2}に代入すると
\begin{align*}
&\lambda^2e^{\lambda x}-\lambda e^{\lambda x}-e^{\lambda x}=0\\
&(\lambda^2-\lambda-1)e^{\lambda x}=0\\
&\lambda^2-\lambda-1=0
\end{align*}となります。
つまり、$y(x)=e^{\lambda x}$が\eqref{2}の解になるためには$\lambda^2-\lambda-1=0$をみたせばよいことが分かります。この2次方程式を解くと
\[
\lambda=\frac{1\pm\sqrt{5}}{2}
\]となります。ということで、$\exp(\frac{1\pm\sqrt{5}}{2}x)$という基本解が見つかりました($e^{\frac{1\pm\sqrt{5}}{2}x}$だと指数が若干重たいので$\exp$で表記しました)。
まず、今求めたいのは基本解です(基本解が求まれば一般解も求まるので)。基本解はどんな手段でもいいから一次独立な解を見つければOKです。なので私が単に「指数関数が解になりそう!」と思ったから$y(x)=e^{\lambda x}$と解の形を決め打ちしてみただけです。もし「2次関数になりそう!」と思ったのであれば、$y(x)=ax^2+bx+c$とおいて\eqref{2}に代入して、$a,b,c$がみたす条件を求めても構いません。しかし、この場合は残念ながら$a=b=c=0$となってしまい、$y(x)=0$という自明な解しか見つかりません。自明な解$0$と任意の関数$y$の組$(0,y)$は一次独立にならないため、$0$は基本解に採用できません。
次に、なぜ「指数関数が解になりそう!」と思ったのかについてです。それは定数係数の斉次1階線形微分方程式$y'(x) + p y(x) = 0$の解が$y(x) = c e^{-p x}\;(c\in\mathbb{R})$と指数関数で表されるからです。定数係数の斉次1階線形微分方程式の解が指数関数だったから、$n$階にしも指数関数になりそうという推論は悪くないと思います。今回はこの推論でうまくいきましたが、ダメだった場合「その方法では上手くいかなかったことが分かった」と思えばいいのではないでしょうか。試行錯誤も数学の醍醐味だと思います。
あと、$\exp(\frac{1\pm\sqrt{5}}{2}x)$が一次独立になっていることの確認もしておきます。簡単のため$\alpha=\frac{1+\sqrt{5}}{2}$,$\beta=\frac{1-\sqrt{5}}{2}$とおきます(当然$\alpha\neq\beta$)。そして
\[
c_1e^{\alpha x}+c_2e^{\beta x}=0
\]がすべての$x\in\mathbb{R}$で成り立つとすると、$x=0,1$の場合でももちろん成り立たなければなりません。つまり
\begin{align*}
&c_1+c_2=0,\\
&c_1e^{\alpha}+c_2e^{\beta}=0
\end{align*}という連立方程式をみたす必要がありますが、これを解くと$c_1=c_2=0$となります。よって$\exp(\frac{1\pm\sqrt{5}}{2}x)$は一次独立でした。
よって、\eqref{2}の一般解は
\begin{align}
y(x)=c_1\exp\left(\frac{1+\sqrt{5}}{2}x\right)+c_2\exp\left(\frac{1-\sqrt{5}}{2}x\right)\label{3}
\end{align}
ここで$f(x)=\sum\limits_{n=0}^{\infty}\frac{F_n}{n!}x^n$について考えていたことを思い出します。$f(0)=F_0=0$,$f'(0)=F_1=1$となるので、\eqref{3}に初期値$y(0)=0$,$y'(0)=1$を与えて$c_1$,$c_2$を決定します。すると
\begin{align*}
y(0)&=c_1+c_2=0,\\
y'(0)&=\frac{1+\sqrt{5}}{2}c_1+\frac{1-\sqrt{5}}{2}c_2=1
\end{align*}なので、これを解くと$c_1=\frac{1}{\sqrt{5}}$,$c_2=-\frac{1}{\sqrt{5}}$となります。
以上より
\begin{align*}
f(x)&=\sum\limits_{n=0}^{\infty}\frac{F_n}{n!}x^n\\
&=\frac{1}{\sqrt{5}}\left(\exp\left(\frac{1+\sqrt{5}}{2}x\right)-\exp\left(\frac{1-\sqrt{5}}{2}x\right)\right)
\end{align*}
言われてみると、最初に見た$f$のグラフは2つの指数関数の和っぽく見えるので、納得感があります。

仕上げに入ります。$\exp(x)=\sum\limits_{n=0}^{\infty}\frac{1}{n!}x^n$となることを使うと
\begin{align*}
\sum\limits_{n=0}^{\infty}\frac{\color{red}{F_n}}{n!}x^n
&=\frac{1}{\sqrt{5}}\left(\exp\left(\frac{1+\sqrt{5}}{2}x\right)-\exp\left(\frac{1-\sqrt{5}}{2}x\right)\right)\\
&=\frac{1}{\sqrt{5}}\left(\sum_{n=0}^{\infty}\frac{1}{n!}\cdot\left(\frac{1+\sqrt{5}}{2}\right)^nx^n - \sum_{n=0}^{\infty}\frac{1}{n!}\cdot\left(\frac{1-\sqrt{5}}{2}\right)^nx^n\right)\\
&=\sum_{n=0}^{\infty}\frac{1}{n!}\cdot\color{red}{\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)}x^n
\end{align*}
\[
F_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)
\]が求まりました。なるほどねえ
まとめ
斉次2階線形微分方程式を解いてフィボナッチ数列の一般項を求めてみました。
今回はフィボナッチ数列に限定して計算しましたが、隣接三項間漸化式$a_{n+2} + p a_{n+1} + q a_n=0$の一般項は$f(x)=\sum\limits_{n=0}^{\infty}\frac{a_n}{n!}x^n$とおくことで全く同様の手順で導出可能です(収束半径を求めるときは$|a_{n+1}|\le2\max\{|p|,|q|\}|a_n|$のような不等式を使うとよいでしょう)。
「特性方程式を解いて$a_{n+2} - \alpha a_{n+1} = \beta(a_{n+1} - \alpha a_n)$と変形する方法」は忘れてしまったが、2階線形微分方程式の解法は覚えている知的生命体はぜひご活用ください。
thank Q for rEaDing.φ(・▽・ )