x=0の周りのTaylor展開がまっったく収束しない関数
f(x)=\sum_{n=0}^{\infty}2^{-n}\cos(n^{2}x)
\]
\[
1+\frac{1}{2}\cos x + \frac{1}{4}\cos 4x + \frac{1}{8}\cos 9x + \cdots
\]のようにコサインたちの和でできている関数となっております。
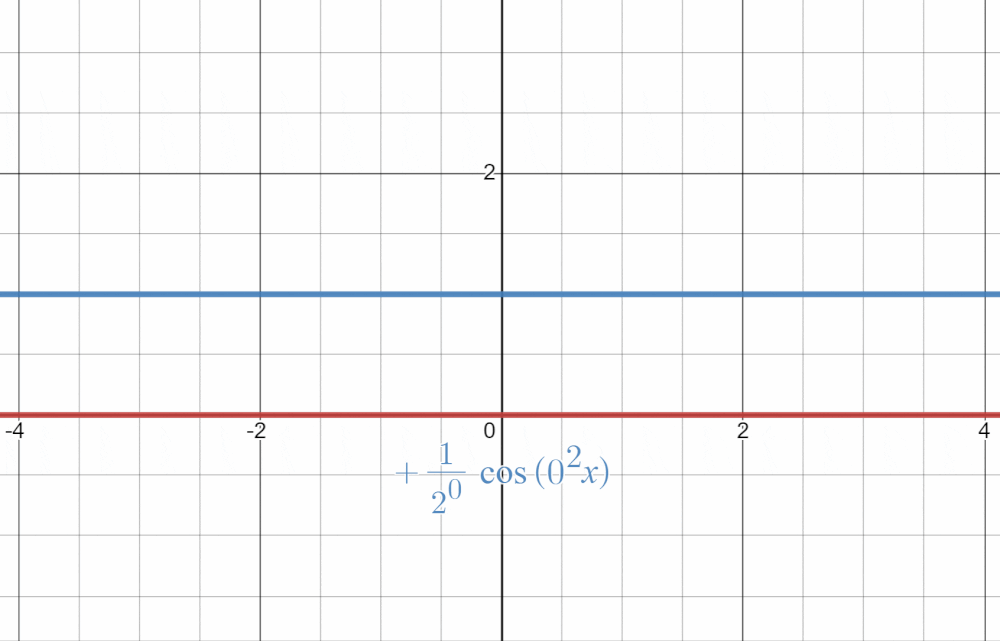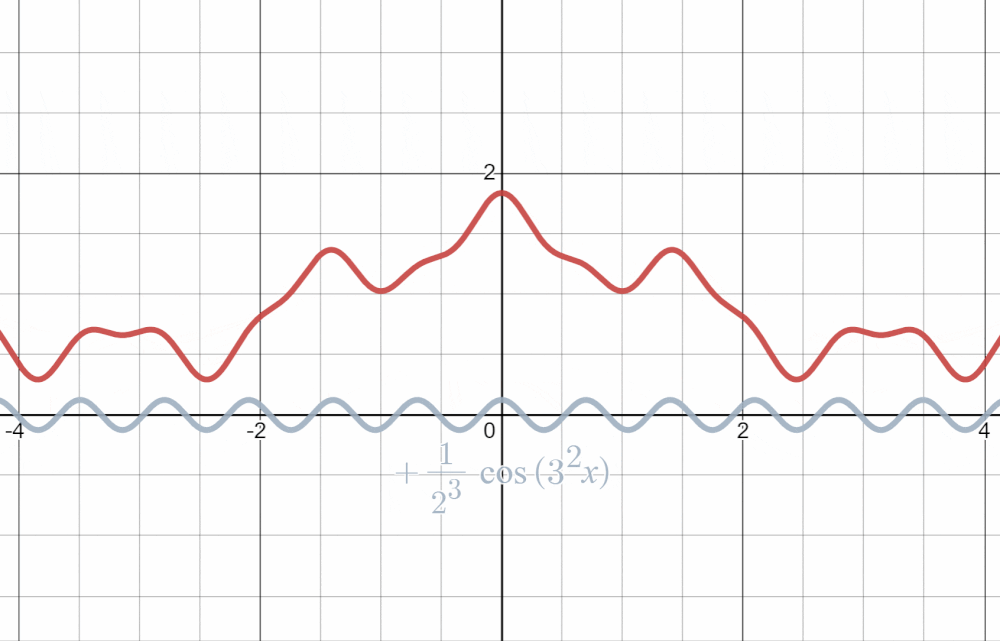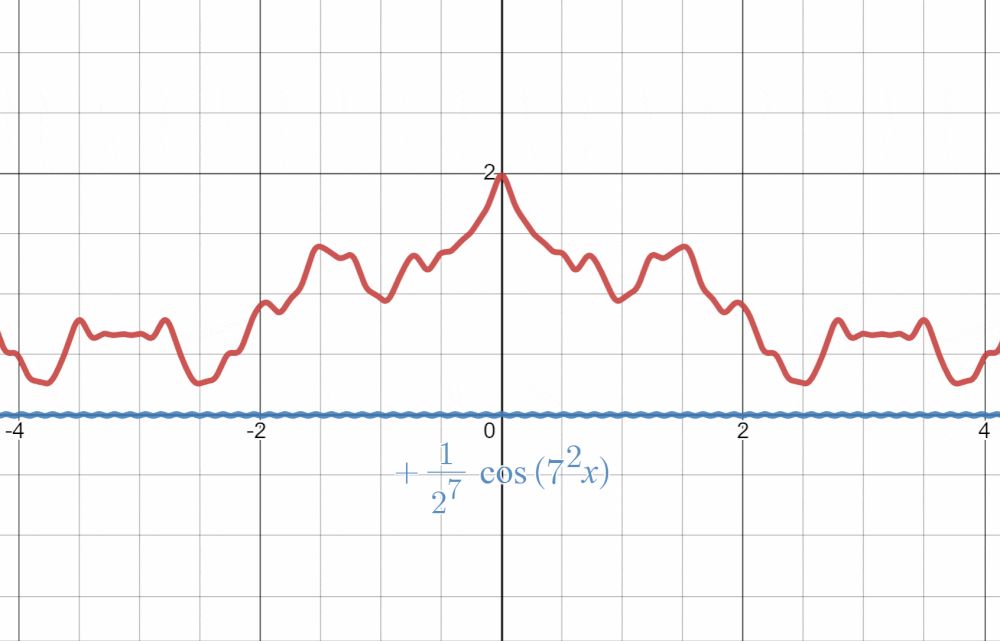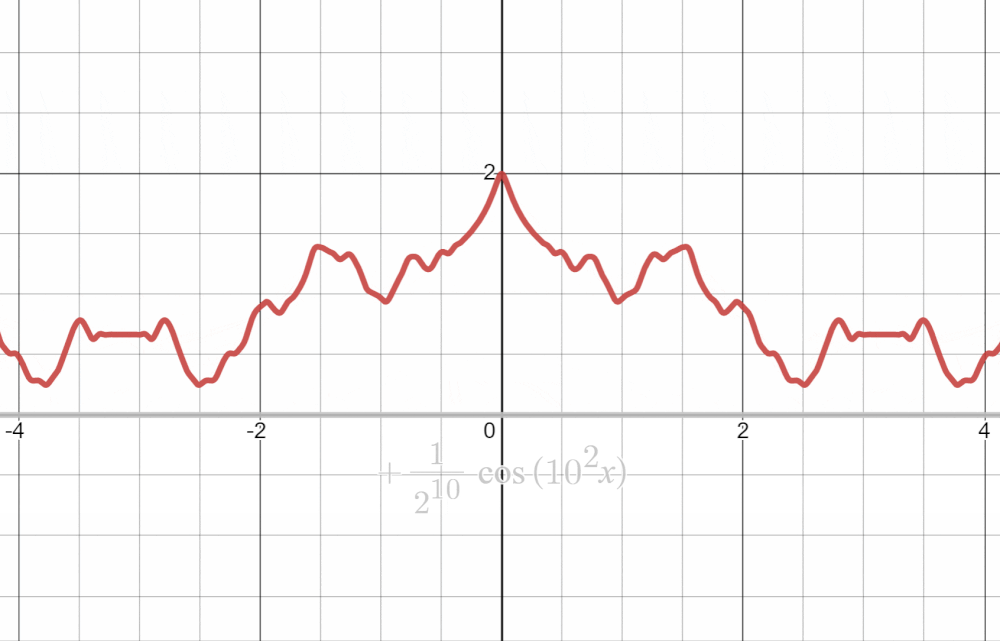
$\cos(n^{2}x)$がグラフの風紀を乱す悪い子となっていますが、$2^{-n}$が抑制してくれているおかげでちゃんと収束しているように見えますね!
とはいえ、関数の無限和(関数項級数)なので、「本当に収束するのか?」という一抹の不安はあります。
でも安心してください。$\sum\limits_{n=0}^{\infty}|a_n|$が収束(絶対収束)すれば、元の級数$\sum\limits_{n=0}^{\infty}a_n$も収束するという事実を用いると、任意の$x\in\mathbb{R}$に対して
\[
\sum_{n=0}^{\infty}|2^{-n}\cos(n^2x)|\le\sum_{n=0}^{\infty}2^{-n}=2
\]となるので、$f(x)$は収束します。
そんな今日の推し関数ですが、次のような著しい性質をもっています:
f(x)=\sum_{n=0}^{\infty}2^{-n}\cos(n^{2}x)
\]は何回でも微分可能($C^{\infty}$級)で,Maclaurin展開($x=0$の周りのTaylor展開)はすべての$x\neq0$で発散する.
\begin{align*}
\left|\sum_{n=51}^{\infty}2^{-n}\cos(n^{2}x)\right|
&\le\sum_{n=51}^{\infty}2^{-n}\\
&=\frac{1}{2^{50}}\\
&\approx8.88\times10^{-16}
\end{align*}となっております(最後の近似値はWolfram Alphaの計算結果を参照しました)。
この見た目で$C^{\infty}$級なのか?すごくいい……!
なにげに周期$2\pi$の周期関数なんだね……!さすがコサインの血を継ぐ子だ……!
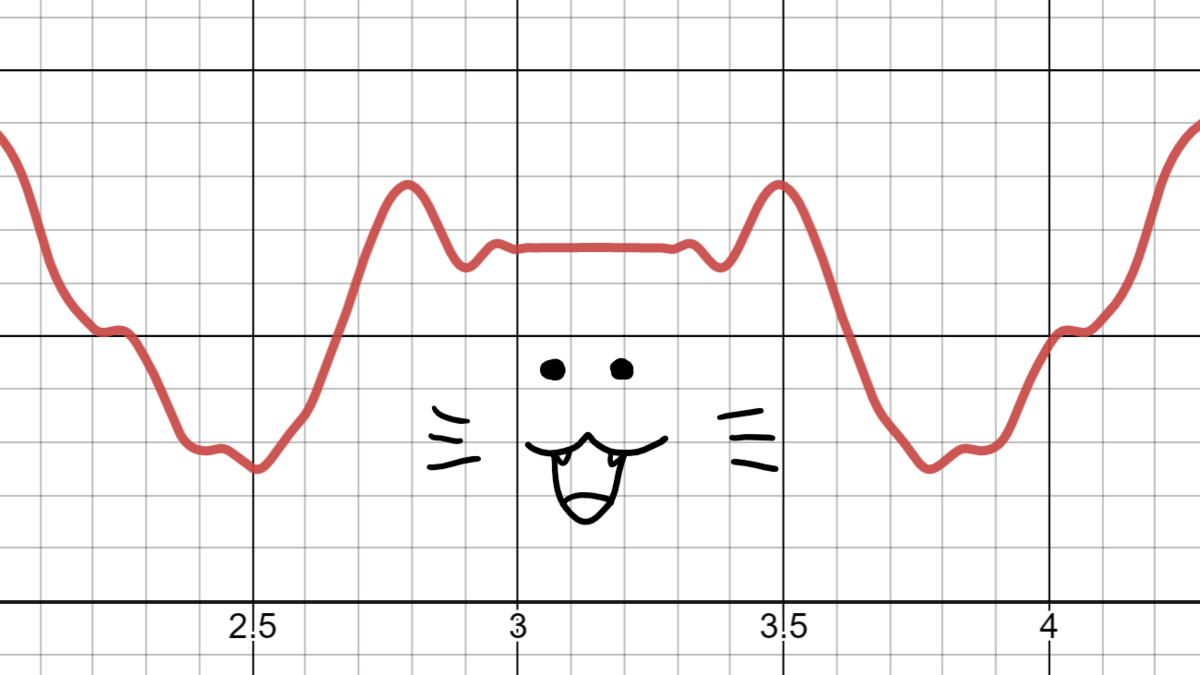
あと、$x=3$周辺が猫ちゃんみたいなグラフをしている所がかわぃい…
Taylor展開の概説
Taylor展開の例
まず最初に、Taylor展開について簡単に説明します。$x=0$の周りのTaylor展開とは、何回でも微分可能な関数$f$に対して
\[
\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\cdots
\]
\[
f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots
\]
多項式関数はもちろん、三角関数、指数関数など、普段お目にかかる関数のTaylor展開は、元の関数に収束していくことが多いです。
\begin{alignat*}{3}
\sin x &= \sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}&=&x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots\\
\cos x &= \sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}x^{2n}&=&1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+\cdots\\
e^x&= \sum_{n=0}^{\infty}\frac{1}{n!}x^{n}&=&1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots\\
\frac{1}{1-x} &=\sum_{n=0}^{\infty}x^n &=& 1+x+x^2+x^3+\cdots\quad(|x|<1)
\end{alignat*}
ただし、$\frac{1}{1-x}$などのように、Taylor展開が収束する範囲と発散する範囲に分かれる場合もあります。
Taylor展開が元の関数に一致しない例
注意したいのは、Taylor展開が収束した場合でも、そのTaylor展開は元の関数に一致するとは限らないということです。よく見かける例としては
\[
f(x)=
\begin{cases}
e^{-1/x} & (x>0)\\
0 & (x\le0)
\end{cases}
\]があります。
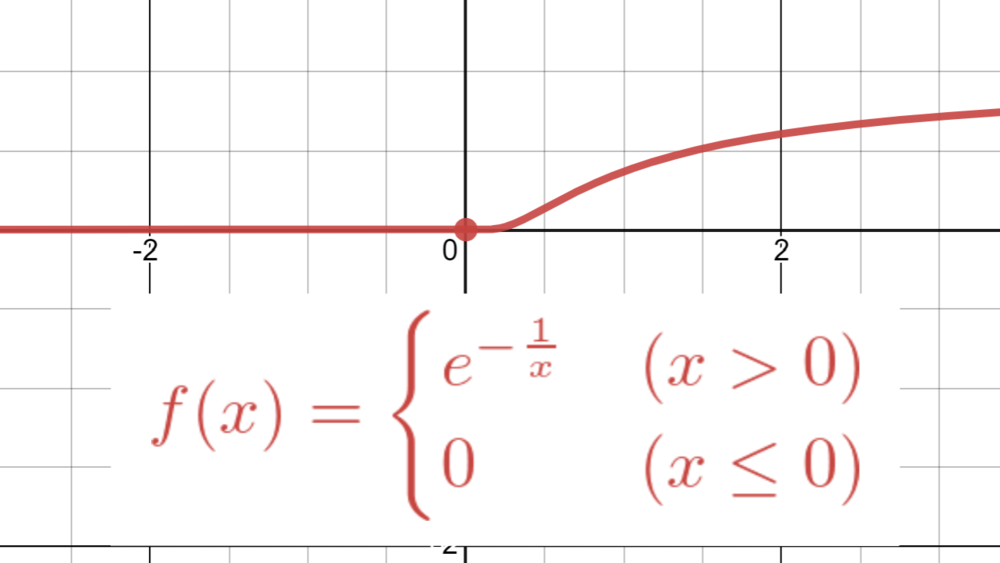
なお、今日の推し関数もTaylor展開が元の関数に一致しない例になっていますが、元の関数に一致するorしない以前に、$x=0$でのTaylor展開が$x\neq0$で収束しない(収束半径が$0$)というオマケが付いてきています。
Taylor展開について軽く抑えたところで、今日の推し関数の微分可能性やTaylor展開について堪能していきましょう。
今日の推し関数の微分可能性
それでは今日の推し関数の微分可能性について考えていきます。
グラフがとげとげしくて微分できなさそうですが、結論から言うと、微分はシグマの中の関数を微分(項別微分)するだけでOKです。
\begin{align*}
f'(x)&=\sum_{n=0}^{\infty}-n^2 2^{-n}\sin(n^{2}x),\\
f''(x)&=\sum_{n=0}^{\infty}-n^4 2^{-n}\cos(n^{2}x),\\
f'''(x)&=\sum_{n=0}^{\infty}n^6 2^{-n}\sin(n^{2}x),\\
\vdots &
\end{align*}厳密なことはひとまずスキップしたい方は、この後の微分可能性に関する証明は読み飛ばしても構いません。ただし、時に「微分可能な関数の無限和は項別微分してヨシ!」の考えは失敗を招くということだけは覚えておいてください。
例えば、至る所微分できない連続関数で有名なWeierstrass関数*1は
\[w(x)=\sum\limits_{n=0}^{\infty}a^n\cos(b^{n}\pi x)\quad(ab>1+\frac{3\pi}{2})\]という形をしています(今日の推し関数に少し似ている!)。コサインは微分できるからヨシ!と思って、
\[w'(x)=-\sum\limits_{n=0}^{\infty}(ab)^n\pi\sin(b^{n}\pi x)\]な~んて計算をすると、嘘つきになりますのでご注意ください。
それでは今日の推し関数の微分可能性を証明します。「こういうときはこの定理が有用です」といった証明のアイデアと方針も含めて書いてみたので、よかったらご覧ください。
\[
\left(\sum_{n=0}^{\infty} f_n\right)'=\sum_{n=0}^{\infty} f'_n
\]が成り立つ.
$f_n(x)=2^{-n}\cos (n^2x)$とおいたとき、$\sum\limits_{n=0}^{\infty} f'_n(x)=\sum\limits_{n=0}^{\infty} -n^2 2^{-n}\sin (n^2x)$が任意の閉区間上で一様収束することを示せば目標達成です。そして、関数項級数の一様収束はWeierstrassのM判定法(優級数定理)が多くの場合で有用です。
- $|g_n(x)|\le M_n\quad(\forall x\in I),$
- $\sum\limits_{n=0}^{\infty}M_n$は収束する.
このとき,$\sum\limits_{n=0}^{\infty}g_n$は$I$上で一様収束する.
\[
|f'_n(x)|\le n^2 2^{-n}
\]という評価ができます(右辺には$x$が現れていないことに注目)。
ここでもし、$\sum\limits_{n=0}^{\infty}n^2 2^{-n}$が収束すればM判定法の条件をみたします!
私の感覚的には収束しそうです。というのも、$n$が十分大きいと$n^2$よりも$2^{-n}$の影響が強くなるため、数列$(n^2 2^{-n})_n$は“ほぼ公比$\frac{1}{2}$の等比数列”と思えるからです。
このように、“ほぼ等比級数”に対してはratio test(D'Alembertの判定法)による判定が有効です*2。
\begin{align*}
\frac{a_{n+1}}{a_n}
&=\frac{(n+1)^2 2^{-n-1}}{n^2 2^{-n}}\\
&=\left(1+\frac{1}{n}\right)^2 \frac{1}{2}\\
&\longrightarrow \frac{1}{2}<1\quad(n\to \infty)
\end{align*}となるため、$\sum\limits_{n=0}^{\infty}n^2 2^{-n}$は収束することが保証されました*3。
以上より、$\sum\limits_{n=0}^{\infty} f'_n(x)=\sum\limits_{n=0}^{\infty} -n^2 2^{-n}\sin (n^2x)$は任意の閉区間上(もっと広く言うと$\mathbb{R}$上)で一様収束します。
ということで、$f(x)=\sum\limits_{n=0}^{\infty} f_n(x)$は項別微分可能で、
\[
f'(x)=\sum_{n=0}^{\infty} -n^2 2^{-n}\sin (n^2x)
\]となることが分かりました。ふー、意外と長かった。
$f'$がさらに微分可能であるかについては、$f'$を形式的に項別微分した$\sum\limits_{n=0}^{\infty} -n^4 2^{-n}\cos (n^2x)$がまた一様収束するかどうかを考えればよいですが、全く同様に証明が可能です。微分する回数を$k$回に増やしても、最終的に$\sum\limits_{n=0}^{\infty}n^{2k} 2^{-n}$が収束するかどうかに行きつきますが、ratio testによって収束することが分かると思います。以上より、今日の推し関数は何回でも微分可能です。
今日の推し関数のTaylor展開
それでは、今日の推し関数の$x=0$の周りのTaylor展開を考えてみましょう。
\begin{align*}
f'(x)&=\sum_{n=0}^{\infty}-n^2 2^{-n}\sin(n^{2}x),\\
f''(x)&=\sum_{n=0}^{\infty}-n^4 2^{-n}\cos(n^{2}x),\\
f'''(x)&=\sum_{n=0}^{\infty}n^6 2^{-n}\sin(n^{2}x),\\
f''''(x)&=\sum_{n=0}^{\infty}n^8 2^{-n}\cos(n^{2}x),\\
\vdots &
\end{align*}となるので、$ m $が奇数のときは$f^{(m)}(0)=0$,$m=2k$(偶数)のときは$f^{(2k)}(0)=\sum\limits_{n=0}^{\infty}(-1)^{k}n^{4k} 2^{-n}$が分かります。よって、\[
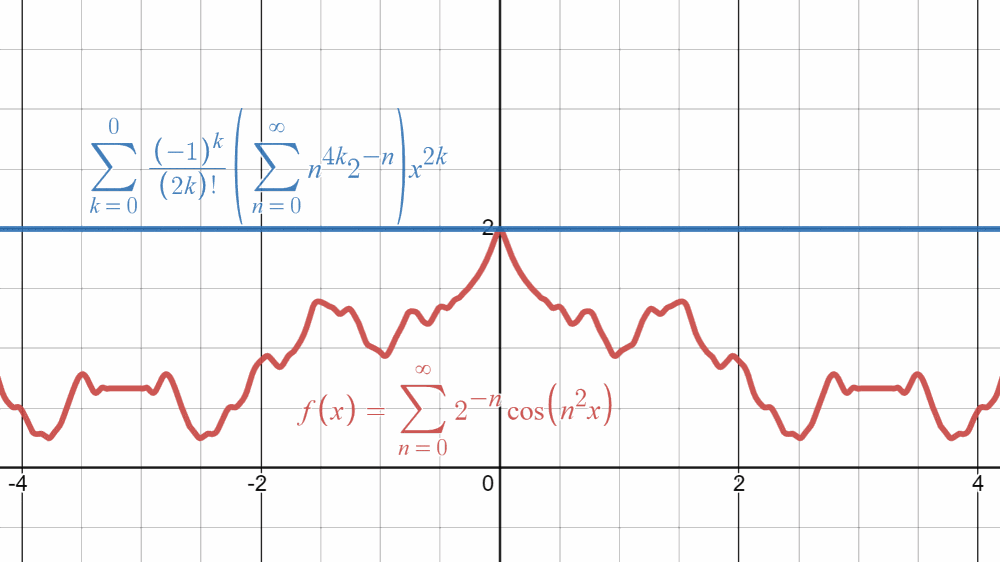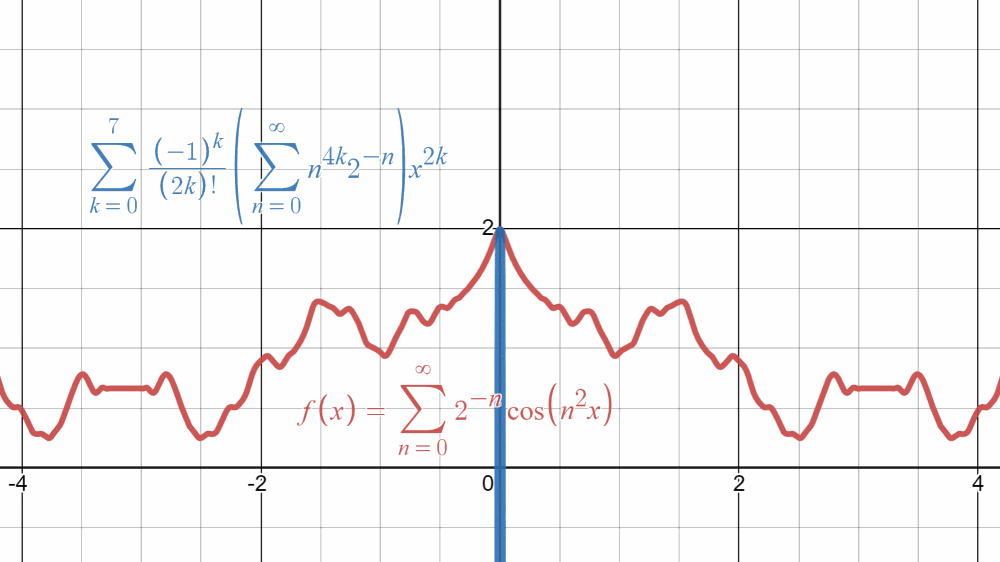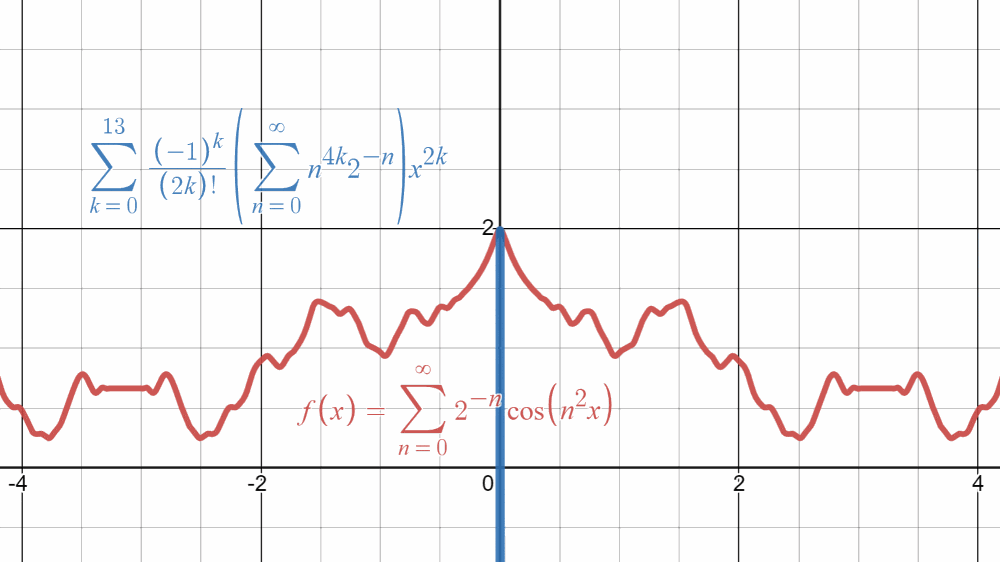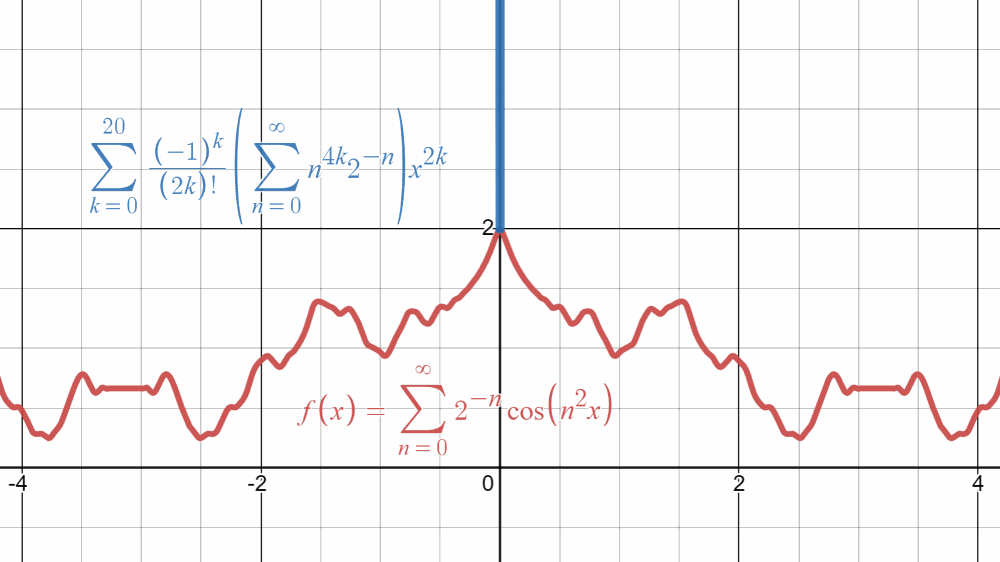
\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k)!}\left(\sum_{n=0}^{\infty}n^{4k} 2^{-n}\right)x^{2k}
\]という$x=0$の周りの(形式的な)Taylor展開が得られました。
このTaylor展開の最初のシグマを$k=0$と$k\ge1$に分けて、$x=0$を代入すれば
\[
\sum_{n=0}^{\infty}2^{-n}=2
\]が出てくるので確かに収束しますし、$f(x)=\sum\limits_{n=0}^{\infty}2^{-n}\cos(n^2x)$に$x=0$を代入したときの値に一致しています。やったね!
では、$x\neq0$の場合ではどうでしょうか?ちゃんと今日の推し関数$f(x)$に一致してくれれば嬉しいのですが、残念ながら発散します(それはそれで嬉しい)。その辺を詳しく見ていきましょう。
Taylor展開の$2k$次の項の係数を
\[
a_{2k}=\frac{(-1)^k}{(2k)!}\left(\sum_{n=0}^{\infty}n^{4k} 2^{-n}\right)
\]とおくと、
\begin{align*}
\left|a_{2k}x^{2k}\right|
& =\frac{1}{(2k)!}\left(\sum_{n=0}^{\infty}n^{4k} 2^{-n}\right)x^{2k}\\
& >\frac{1}{2k^{2k}}N^{4k} 2^{-N}x^{2k}\\
& =\left(\frac{N^2x}{2k}\right)^{2k}2^{-N}
\end{align*}となります($N=1, 2, 3, \ldots$)。
- $n! < n^n$
- $c_n > 0$のとき$\sum\limits_{n=0}^{\infty}c_n > c_N$(1個だけ選ぶ)
を用いました。
したがって、$x\neq0$のときは$k > \frac{1}{|x|}$をみたす自然数$k$を考えて$N=2k$とすれば
\begin{align*}
\left|a_{2k}x^{2k}\right|
& >\left(\frac{N^2x}{2k}\right)^{2k}2^{-N} \\
& =(2kx)^{2k}2^{-2k}\\
& > 1
\end{align*}となります。これは、数列$(a_{2k}x^{2k})_k$が$k\to\infty$のとき$0$に収束しないことを意味するので、今日の推し関数のTaylor展開$\sum\limits_{k=0}^{\infty}a_{2k}x^{2k}$は$x\neq0$では発散することが分かります($\sum\limits_{n=0}^{\infty}c_n$が収束するならば$c_n\to0\;(n\to\infty)$の対偶)。
いやー、こんなに収束したい気持ちを振り切ったTaylor展開は見たことなかったです。
ブラボー!ブラボー!ブラボー!!!!
まとめ
本日は、$x=0$の周りのTaylor展開がまっったく収束しない関数を紹介しました。無限和ではあるものの、実質コサインだけでこんなに変わった性質をもった関数ができるのは面白いですね。
#今日の推し関数はTwitterで毎週金曜か土曜に少なくとも一回投稿する予定です。
気が向いたら過去の推し関数をブログにしようと思いますのでよろしくお願いします!
thank Q for rEaDing.φ(・▽・ )
おまけ:他の点の周りのTaylor展開は?
おまけというか、個人的に分かっていないところを包み隠さずまとめておきます。
本日は今日の推し関数の$x=0$の周りのTaylor展開について話しました。ここまで来たら$x=a$での周りのTaylor展開についても気になるところですが、実際に書き下すと
\[
\sum_{k=0}^{\infty}\frac{(-1)^{\lfloor(k+1)/2\rfloor}}{k!}\sum_{n=0}^{\infty}n^{2k}2^{-n}\cos\left(n^2a+\tfrac{(-1)^{k}-1}{4}\pi\right)(x-a)^k
\]
また、コサインの中身にある$\frac{(-1)^{k}-1}{4}\pi$は、微分したときのサインコサインの切り替えるためのものになっています。
例えば$x=0.5$の周りのTaylor展開($k=21$次で打ち止め)はこのようになります。

今日の推し関数の無限和の部分を有限($n=50$まで)で止めている図になっていることもあり、ちょっと収束しているように見えています。
この図が、$x=0.5$の周りのTaylor展開がわずかに狭い範囲で収束することを示唆しているのか、はたまた$x\neq0.5$でまっったく収束しないのかは分かっていません。
最終的には、$x=a$の周りのTaylor展開の収束半径を知りたいんですけど、私の計算力が足りませんでした。$x=0$の場合と同じ方針で
\[
\frac{1}{k!}\left\lvert\sum_{n=0}^{\infty}n^{2k}2^{-n}\cos\left(n^2a+\tfrac{(-1)^{k}-1}{4}\pi\right)\right\rvert\lvert x-a\rvert^k
\]を、$k$に依存しない正の定数で下から評価できればいいのですが…(本当にできるのか?)。
何か分かったら追記します。
参考文献など
- Bernard R. Gelbaum, John M. H. Olmsted, Counterexamples in Analysis, Dover Publications
また、関数の足し合わせのgifの演出は、もっちょさんの以下のツイートを真似たものになっています:
黒をどんどん足し合わせていくとだんだん赤になっていくcosのマクローリン展開 pic.twitter.com/OpPOcY9GW6
— 鯵坂もっちょ🐟『つれづれなる数学日記』好評発売中! (@motcho_tw) 2019年3月4日