「足してA、引いてB」と「運命の赤い関数」

「足してA、引いてBになる2つの数」に関するお話の前編です。今回は「運命の赤い関数」を作ります。お楽しみに！

あと、今回は一度やってみたかった「対話形式」で書いてみました。

登場人物

マスマスさん：数学を学ぶ男子大学生。コロリーの家に居候している。最近、病的な関数に興味をもっている。

コロリー：数学が好きなゆるキャラ。数学をマスマスさんに教わっている。数学のあとに舐めるハチミツが生きがい。

第1章「足してA、引いてBって？」

コロリー「マスマスさんw 今日は大学行かないの？w」

マスマス「うん、大学はもう授業がないんだ。試験も終わって暇だから、病的な関数を作って遊んでいたんだ」

コロリー「え？何それw 教えて教えてw」

マスマス「ん～しょうがないな～。…じゃあね、まずはこんな問題を考えてみよっか？」

問題

足して $A$ ，引いて $B$ になる2つの数，つまり\begin{cases}
x+y=A\\
x-y=B
\end{cases}を満たす $x$ ， $y$ を求めなさい．

コロリー「マスマスさんw これって連立方程式？簡単だよw」

マスマス「じゃあ解いてごらん。文字がたくさんあるけど、求めたいものは何なのかを忘れないようにね。 $x$ と $y$ を求めたいから、答えは
\begin{equation}x=(AとBの式)，y=(AとBの式)\end{equation}という形で答えるんだよ」

コロリー「うん、わかったw えっと、この場合、上の式と下の式を足せば $y$ が消えるね。
\begin{equation}2x=A+B\end{equation}になったから、
\begin{equation}x=\dfrac{A+B}{2}\end{equation}かな？」

マスマス「正解！」

コロリー「よぅしw 次はこれを、上の式に代入するぞお。

\begin{align*}
\dfrac{A+B}{2}+y &=A &&(x=\frac{A+B}{2}を代入した)\\
y &=A-\dfrac{A+B}{2} &&(\frac{A+B}{2}を移項した)\\
y &=\dfrac{2A-(A+B)}{2} &&(通分した)\\
y &=\dfrac{A-B}{2} &&(計算した)
\end{align*}

どう？合ってる？マスマスさん？」

マスマス「うん！大正解！」

コロリー「おぅw やったーwww」

マスマス「実はね、 $x=\dfrac{A+B}{2}$ を代入するよりも
\begin{cases}
x+y=A\\
x-y=B
\end{cases}に戻って、 $(上の式)-(下の式)$ を計算したほうが簡単だったんだ」

コロリー「えぇ？あっ、本当だw
\begin{equation}2y=A-B\end{equation}になるから、
\begin{equation}y=\dfrac{A-B}{2}\end{equation}となった！」

マスマス「そうそう。いつでも『どうすればラクして計算できるかな？』という気持ちを忘れずにね。それはともかく、今の計算で次のことが分かったね」

足してA，引いてB

$\frac{A+B}{2}$ と $\frac{A-B}{2}$ は足してA，引いてBになる．つまり，\begin{cases}
\dfrac{A+B}{2}+\dfrac{A-B}{2}=A\\
\dfrac{A+B}{2}-\dfrac{A-B}{2}=B.
\end{cases}

コロリー「連立方程式に代入したんだね。なるほどねぇw」

第2章「運命の赤い関数」

コロリー「で、これがどうかしたの？w」

マスマス「突然だけど、コロリーは『運命の赤い糸』って知ってる？」

コロリー「え、知ってるよw 人は運命の人と見えない糸で結ばれてるという言い伝えでしょ？見えないのに赤いんだよねw 赤外線かなw」

マスマス「でね、今日は足してA、引いてBを使って、『運命の赤い糸』を作るよ！」

コロリー「えぇっ！そんなことできるの？」

マスマス「『運命の赤い関数』と言ったほうが正確かな。要するに、こんな関数のことだよ」

f:id:corollary2525:20170204202849p:plain

コロリー「うぉう、ハートができてる！すごいよマスマスさん！」

マスマス「よし、コロリーも一緒に作ろう！」

コロリー「やったぁーw」

マスマス「まずはハートの上の部分の関数を作ろう。」

f:id:corollary2525:20170204204636p:plain

マスマス「コロリーは何に見える？」

コロリー「ん～、円がふたつかなぁ～」

マスマス「いいねぇ！じゃあ円を考えよっか。円の方程式は $x^2+y^2=r^2$ で表せたね。これを $y$ について解くと
\begin{equation}
y=\pm\sqrt{r^2-x^2}
\end{equation}となるよ」

コロリー「ふむ。 $x^2$ を移項して、ルートをとったんだね」

マスマス「そうそう。で、今は円の上側の式が欲しいからプラスの方を選ぼう。半径は $r=1$ としておくと\begin{equation}y=\sqrt{1-x^2}\end{equation}という式になるね。グラフにするとこうなるよ」

f:id:corollary2525:20170204211049p:plain

コロリー「ふむふむ」

マスマス「そして、 $x$ 軸方向に1だけ平行移動させるよ。これは $x$ の部分を $x-1$ に書き換えればいいんだ。すると、
\begin{equation}
y=\sqrt{1-(x-1)^2}
\end{equation}という式になるね」

f:id:corollary2525:20170204211937p:plain

コロリー「ん～なるほどぉ。じゃあもう一つの円は $x$ 軸方向に $-1$ だけ平行移動させればいいんだぁね。ということは
\begin{equation}
y=\sqrt{1-(x+1)^2}
\end{equation}がもう一つの円の方程式だね？マスマスさん！」

マスマス「うん！それでもいいけど、
\begin{equation}
y=\sqrt{1-(|x|-1)^2}
\end{equation}と書くだけで円を2つとも表せるんだ」

コロリー「えぇ？本当かなぁ？」

マスマス「場合分けして考えてみよっか。 $x>0$ のときは絶対値はそのまま外れて
\begin{equation}
y=\sqrt{1-(x-1)^2}
\end{equation}という式になるよね。 $x<0$ のとき、絶対値を外すときはマイナスが付くけど、
\begin{eqnarray*}
y&=&\sqrt{1-(-x-1)^2}\\
&=&\sqrt{1-(x+1)^2}
\end{eqnarray*}となるよ」

コロリー「わ！？僕の作った式とおんなじだぁ！」

マスマス「ということで、ハートの上の部分ができたね。 $a(x)$ と名付けておこう」

f:id:corollary2525:20170204213233p:plain

マスマス「次はハートの下の部分を考えよう」

f:id:corollary2525:20170204214108p:plain

コロリー「うーん。難しいなあ」

マスマス「難しかったら別のにするかい？例えば、こんなハートもかわいいと思うよ」

f:id:corollary2525:20170204220054p:plain

コロリー「おお！これならできそうw えっと、この場合は、半径2の円がいいのかな？」

マスマス「うんうん」

コロリー「半径2の円の方程式は $x^2+y^2=4$ だから、
\begin{equation}y=\pm\sqrt{4-x^2}\end{equation}となって、今は円の下側を使いたいから\begin{equation}y=-\sqrt{4-x^2}\end{equation}かな？」

マスマス「うん。合っているよ！じゃあこの関数を $b(x)$ と名付けようか」

f:id:corollary2525:20170204223833p:plain

コロリー「でも、これを作ってこのあとどうするの？『運命の赤い糸』ホントに作れるの？」

マスマス「ここで足してA、引いてBが活躍するんだ！コロリーにちょっと質問するけど、
\begin{equation}\dfrac{a(x)+b(x)}{2}+\dfrac{a(x)-b(x)}{2}\end{equation}は何になるかわかるかい？」

コロリー「ええと、このまま足せばいいのかな？

\begin{align*}
\dfrac{a(x)+b(x)}{2}+\dfrac{a(x)-b(x)}{2} &=\dfrac{a(x)+b(x)+a(x)-b(x)}{2}\\
&=\dfrac{2a(x)}{2}\\
&=a(x)\end{align*}

あっ、 $a(x)$ になったw」

マスマス「そうだね。これは、足してA、引いてBの『足してA』の部分なんだ。 $A=a(x)$ 、 $B=b(x)$ として書き換えたものを書くとこうなるよ」

足して $a(x)$ ，引いて $b(x)$

\begin{cases}
\dfrac{a(x)+b(x)}{2}+\dfrac{a(x)-b(x)}{2}=a(x)\\
\dfrac{a(x)+b(x)}{2}-\dfrac{a(x)-b(x)}{2}=b(x)
\end{cases}

コロリー「ここで足してA、引いてBを使うんだぁね」

マスマス「最後に、もうひと工夫をするよ。
\begin{equation}
F(x)=\dfrac{a(x)+b(x)}{2}+c(x)\cdot\frac{a(x)-b(x)}{2}
\end{equation}という関数 $F(x)$ を考えよう。ここで、もし $c(x)=1$ だったら『足してA』の形に、 $c(x)=-1$ だったら『引いてB』の形になるのは分かるかい？

コロリー「えっと…うん、確かに！」

マスマス「コロリー、最後の質問！『1になったり、-1になったりする関数』って思いつく？」

コロリー「『1になったり、-1になったりする関数』かぁ…。あっ！分かった！ $\sin x$ だね！」

マスマス「そう！その通り！もちろん $\cos x$ でもOKだよ。ということで、『運命の赤い関数』の完成！」

運命の赤い関数（？）

$a(x)=\sqrt{1-(|x|-1)^2}$ ， $b(x)=-\sqrt{4-x^2}$ とする．このとき，

\begin{equation}
F(x)=\dfrac{a(x)+b(x)}{2}+\sin x\cdot\dfrac{a(x)-b(x)}{2}
\end{equation}

は運命の赤い関数である（？）

コロリー「マスマスさん！早くグラフをみせてよ！」

マスマス「数式を書いてるからちょっと待っててね…はい！できました！」

f:id:corollary2525:20170205000120p:plain

コロリー「な、なにこれぇ！？マスマスさんの嘘つき！全然ハートになんかなってないじゃないか！」

マスマス「あっはは、ごめんごめん。 $\sin x$ の周期をもっと短くしないと駄目だったね。 $\sin x$ の中身を $50x$ くらいに書き換えてっと」

運命の赤い関数

$a(x)=\sqrt{1-(|x|-1)^2}$ ， $b(x)=-\sqrt{4-x^2}$ とする．このとき，

\begin{equation}
F(x)=\dfrac{a(x)+b(x)}{2}+\sin50x\cdot\dfrac{a(x)-b(x)}{2}
\end{equation}

は運命の赤い関数である．
f:id:corollary2525:20170205001845p:plain

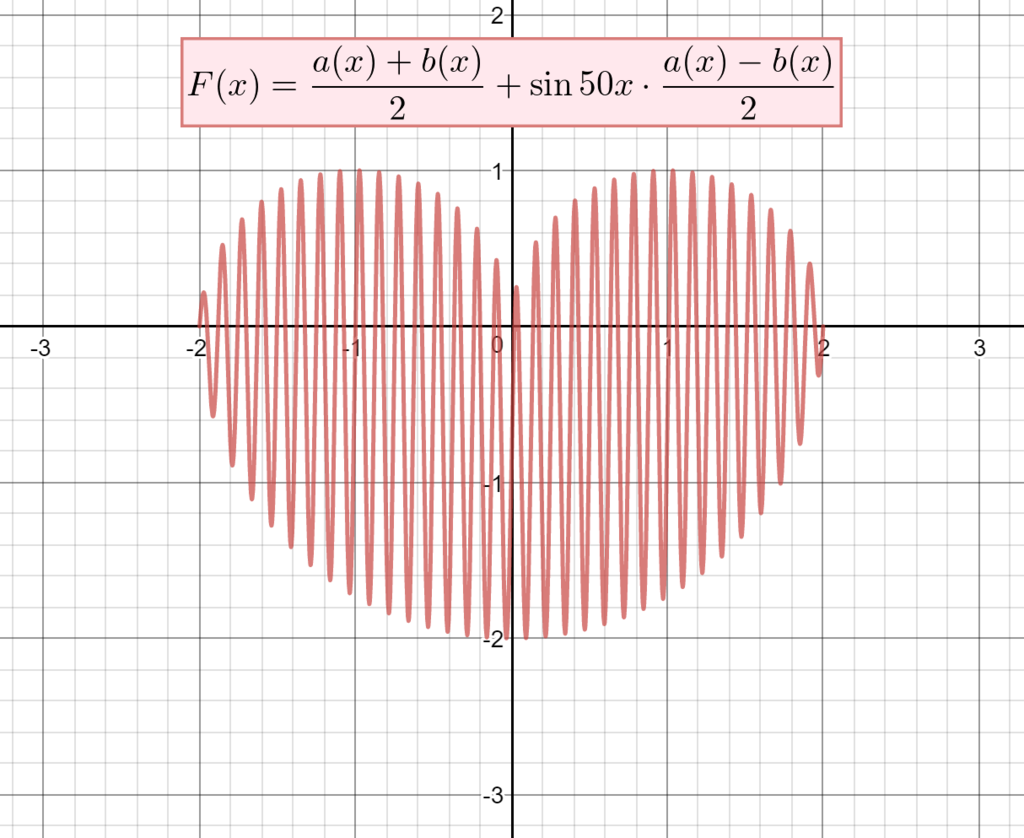
コロリー「うわw すごい！ハートになってるw」

マスマス「でしょ？ちなみに、僕がさっき作ったハートの関数の下側は
\begin{equation}b(x)=\sin^{-1}(|x|-1)-\dfrac{\pi}{2}\end{equation}として作ったんだ。 $\sin^{-1}x$ は $\dfrac{1}{\sin x}$ のことじゃなくて、 $\sin x$ の逆関数 ${\rm arcsin}\;x$ のことだよ」

コロリー「ふーん。よくわかんないからまた今度教えてw このハート、コロネに見せてくるw じゃあね！マスマスさん！」

マスマス「えっちょまっ！…ああ、行っちゃった。本当はこっちを見せたかったんだけどなあ」

f:id:corollary2525:20170205011648p:plain

マスマス「 $\sin x$ の代わりに、 $\cos\left(\dfrac{1}{x}\right)$ を使った『運命の赤い関数』。 $F(0)=-1$ と別途で定義してあげれば*1、『弧状連結ではない連結な関数』になる。連続にはなれない。でも連結にならなれる。計算してないけど、糸の距離も無限だろう。ああ…こんなにも愛しくて切ない関数…君に出会えてよかった…！」