Smooth maximumを作って遊ぼう - Corollaryは必然に。

以前、maxやminを使って数式お絵描きをする記事を書きました。
corollary2525.hatenablog.com

要約すると、2つの不等式
\begin{align*}
\color{red}{f(x,y)}\ge0,\\
\color{blue}{g(x,y)}\ge0
\end{align*}を
\begin{equation*}
\min(\color{red}{f(x,y)}, \color{blue}{g(x,y)})\ge0
\end{equation*}のように $\min(\cdot,\cdot)\ge0$ でまとめると、領域 $f(x,y)\ge0$ と $g(x,y)\ge0$ の共通部分を表す領域になり、「 $=0$ 」にするとその境界を表します。
f:id:corollary2525:20191211185647p:plain

同じように、
\begin{equation*}
\max(\color{red}{f(x,y)}, \color{blue}{g(x,y)})\ge0
\end{equation*}のように $\max(\cdot,\cdot)\ge0$ でまとめると、領域 $f(x,y)\ge0$ と $g(x,y)\ge0$ の和集合を表す領域になり、「 $=0$ 」にするとその境界を表します。

f:id:corollary2525:20191211185654p:plain

f:id:corollary2525:20191211185700p:plain

f:id:corollary2525:20191211185713p:plain

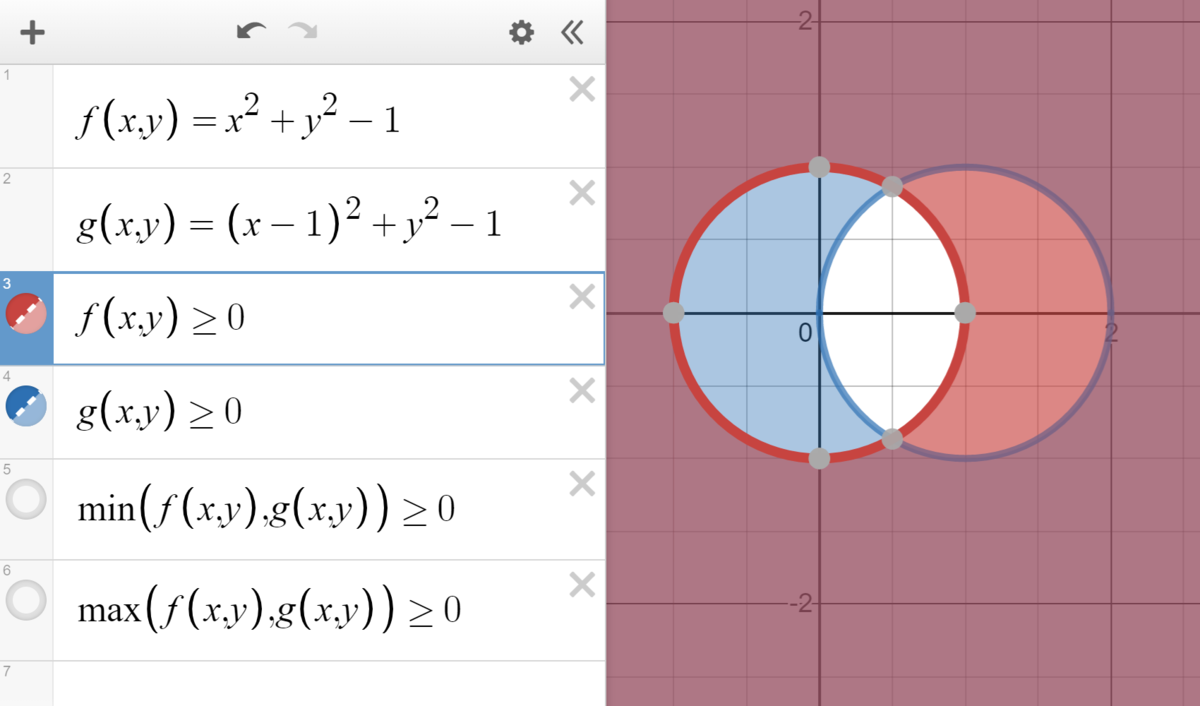
なお、 $x^2+y^2\ge r^2$ は円の外部の領域を表す不等式であるため、和集合をとる操作と共通部分をとる操作を間違えやすいので注意しましょう。必要であれば
\begin{equation*}
f(x,y)=-(x^2+y^2-r^2)
\end{equation*}とおいてみると良いかもしれません。このとき $f(x,y)\ge0$ は不等号が反転して円の内側の領域を表すようになるので、論理と集合で習ったベン図のように扱えます。
f:id:corollary2525:20200725212610p:plain

さて、本日はmax関数とよく似た関数であるSmooth maximumで遊ぼうと思います。

Smooth maximumとその例
Smooth maximumの作り方
Smooth maximumを用いて数式お絵描き
a→∞のとき一様にLSE_a→max
a→∞のとき一様にS_a→max？
まとめ
参考文献など

Smooth maximumとその例

数式お絵かきにこだわっていると、2つ以上の曲線をなめらかにつなぎたいことがよくあります。例えば次のように2つの円をなめらかにつなぐ場合です。
f:id:corollary2525:20200719151545p:plain

このような曲線をシンプルな式で表現してみることを考えてみます。冒頭で説明した通り、max関数を使えば2つの円をつなぐことが可能でした。ということは、Smooth maximumと呼ばれる「max関数をなめらかに近似したもの」があれば、2つの円をなめらかにつなぐことを実現できそうです。

より正確に言うと、Smooth maximumとは関数列 $(m_{a})_{a>0}$ のことであって、

任意の $a > 0$ に対して $m_{a}:\mathbb{R}^N\to\mathbb{R}$ はなめらか
$a\to\infty$ のとき $m_{a}\to\max$

をみたすものを言います。

補足　ちなみに、Smooth maximum $(m_{a})_{a}$ はSmooth minimumにもなっていること、つまり

任意の $a < 0$ に対して $m_{a}:\mathbb{R}^N\to\mathbb{R}$ はなめらか
$a\to-\infty$ のとき $m_{a}\to\min$

となるケースがあるようです。

上記をみたす関数列はいくらでもあるのですが、この記事では2つのSmooth maximumを紹介したいと思います。

LogSumExp関数

まずは1つ目のSmooth maximumです。

定義（LogSumExp関数）

$a > 0$ とする．LogSumExp関数 $\operatorname{LSE}_{a}:\mathbb{R}^N\to\mathbb{R}$ を

$\operatorname{LSE}_{a}(x_1, x_2, \ldots, x_N):=\displaystyle\frac{1}{a}\log\left(\sum_{i=1}^N e^{a x_i}\right)$

によって定義する．特に， $2$ 変数の場合は

$\operatorname{LSE}_{a}(x_1, x_2)=\dfrac{1}{a}\log\left(e^{a x_1}+e^{a x_2}\right).$

ログ！サム！エクスポネンシャル！数式見たまんまのネーミングですね。なお、数式お絵かきのようにPCに計算させることを考慮すると、 $|x_i|$ が大きすぎると $e^{a x_i}$ の計算でoverflow，underflowする可能性があります。そこで $x_{\max}:=\max(x_1,x_2,\ldots,x_N)$ とおくと

\begin{align*}
\frac{1}{a}\log\left(\sum_{i=1}^Ne^{a x_i}\right)
&= \frac{1}{a}\log\left(e^{a x_{\max}}\sum_{i=1}^N e^{a(x_i - x_{\max})}\right) \\
&= x_{\max} + \frac{1}{a}\log\left(\sum_{i=1}^N e^{a(x_i - x_{\max})}\right)
\end{align*}

という指数の肩を軽くする表示ができるので、overflow，underflowする可能性を下げることができます。ついでにこの式から $\operatorname{LSE}_a$ が $\max$ にそこそこ近いことが読み取れると思います。

また、他の記事によっては「 $\operatorname{LSE}$ 」を $\operatorname{LSE_{1}}$ の意味で使ったり $\operatorname{LSE}_{a}$ の意味で使ったりすることがあるのでご注意ください。

多変数Swish関数（仮）

もう一つSmooth maximumをご紹介します。

定義（多変数Swish関数）

$a > 0$ とする．multivariable Swish関数 $S_{a}:\mathbb{R}^N\to\mathbb{R}$ を

\begin{equation*}
S_{a}(x_1, x_2, \ldots, x_N):=\dfrac{\sum_{i=1}^N x_i e^{a x_i}}{\sum_{i=1}^N e^{a x_i}}
\end{equation*}

によって定義する．特に， $2$ 変数の場合は
\begin{equation*}
S_{a}(x_1,x_2)=\frac{x_1e^{a x_1}+x_2e^{a x_2}}{e^{a x_1}+e^{a x_2}}.
\end{equation*}

「multivariable Swish関数」は私が勝手に名付けました（正式名称をご存知の方がいましたら教えていただけると幸いです）。名前の由来はLogSumExp関数のことを「multivariable softplus」とも呼ぶらしいので、それに倣いました。「Softplus」「Swish」については後ほど紹介します。

こちらも指数の計算でoverflow，underflowする可能性を下げたければ

\begin{align*}
\dfrac{\sum_{i=1}^N x_i e^{a x_i}}{\sum_{i=1}^N e^{a x_i}}&=\dfrac{e^{ax_{\max}}\sum_{i=1}^N x_i e^{a (x_i-x_{\max})}}{e^{ax_{\max}}\sum_{i=1}^N e^{a (x_i-x_{\max})}}\\
&=\dfrac{\sum_{i=1}^N x_i e^{a (x_i-x_{\max})}}{\sum_{i=1}^N e^{a (x_i-x_{\max})}}
\end{align*}

と式変形しておくとよいと思います。

ちなみに、Deep learning等で使われるSoftmax関数 $\sigma:\mathbb{R}^N\to\mathbb{R}^N$ ，

$\sigma(x)=\dfrac{1}{\sum_{i=1}^N e^{x_i}} \begin{pmatrix} e^{x_1}\\ e^{x_2}\\ \vdots\\ e^{x_N} \end{pmatrix}$

を用いると

$S_{a}(x)=x^T\sigma(a x)$

と表すことができます（ $x^T$ は $x$ の転置）。

補足　 $\mathbb{R}^N$ の内積をドットで表すのであれば $S_{a}(x)=x\cdot\sigma(a x)$ でもよいでしょう。

初見ではよく分からん

結論を言ってしまうと、今ご紹介したLogSumExp関数またはmultivariable Swish関数をmax関数の代わりに使えば、2つ以上の曲線をなめらかにつなぐことができます。しかし、初見ではこれらの関数がmax関数をなぜなめらかに近似するのか、なぜそのような関数を思いつくことに至ったのか、よく分からないと思います。少なくとも私自身は初めてLogSumExp関数を見たとき、仕組みがよく分からなかったですし、今まで仕組みがよく分からないままLogSumExp関数を使って数式お絵かきをしていました。

正体および出所が不明の関数を使うのは釈然としないと思う方のためにも、まずはLogSumExp関数およびmultivariable Swish関数について詳しく説明したいと思います。また、記事の最後で関数列 $(\operatorname{LSE}_a)_{a > 0}$ ， $(S_a)_{a > 0}$ が $\max$ に収束することを証明するので必要であればご覧ください。

Smooth maximumの作り方

簡単のため、しばらくmax関数などは2変数で考えます（ $N=2$ ）。

Step1 目標は「なめらかな絶対値」

そもそも $\max(x,y)$ は場合分けで定義された関数です。場合分けなしの式でSmooth maximumを作るのは難しいように思えますが、 $\max(x,y)$ は絶対値を用いて
\begin{equation*}
\max(x,y)=\dfrac{1}{2}(x+y+\lvert x-y\rvert)
\end{equation*}と表すことができます。 $x>y$ ， $x\le y$ で場合分けして絶対値を外すと…おぉ確かに合っていますね（ちなみにminの方は $\min(x,y)=\frac{1}{2}(x+y-\lvert x-y\rvert)$ ）。

ということはですよ…？「なめらかに近似された絶対値」を作ることができれば、Smooth maximumを作れると思いませんか？

では、「なめらかな絶対値」を作りましょう！

…なめらかな絶対値って何？

Step2 絶対値の素「Softplus関数」「Swish関数」

ところで、私の浅はかな知見ですが、機械学習やDeep learningでは活性化関数と呼ばれる関数が出てきます。この活性化関数について調べていたときに、Softplus関数
\begin{equation*}
f(x)=\log(1+e^x)
\end{equation*}とSwish関数
\begin{equation*}
g(x)=\dfrac{x}{1+e^{-x}}
\end{equation*}という関数があることを知りました。
f:id:corollary2525:20200719234635p:plain

グラフ（および式）を見れば確かになめらかであり、 $x\to-\infty$ のとき $f(x)\to0$ ， $g(x)\to0$ となることが分かります。 $x\to\infty$ のときは
\begin{align*}
f(x)&= x+\log(1+e^{-x}),\\
g(x)&= x-\dfrac{x}{1+e^x}
\end{align*}であるから直線 $y=x$ に近づいていくことが分かります。

つまり、Softplus関数やSwish関数は「絶対値の正の部分の関数」
\begin{align*}
\varphi(x)&=
\begin{cases}
0 & (x\le 0)\\
x & (x >0)
\end{cases}\\
&=\max(0,x)
\end{align*}をなめらかに近似していると言えます。そこで、Softplus関数やSwish関数に適切なパラメータ $a>0$ を付与して、 $a\to\infty$ のときに関数 $\varphi$ に収束するようなものを考えます。

こうしてできた関数がコチラになります：

\begin{align*}
f_{a}(x)&=\frac{1}{a}\log(1+e^{a x})\\
g_{a}(x)&=\frac{x}{1+e^{-a x}}
\end{align*} f:id:corollary2525:20200719180919p:plain

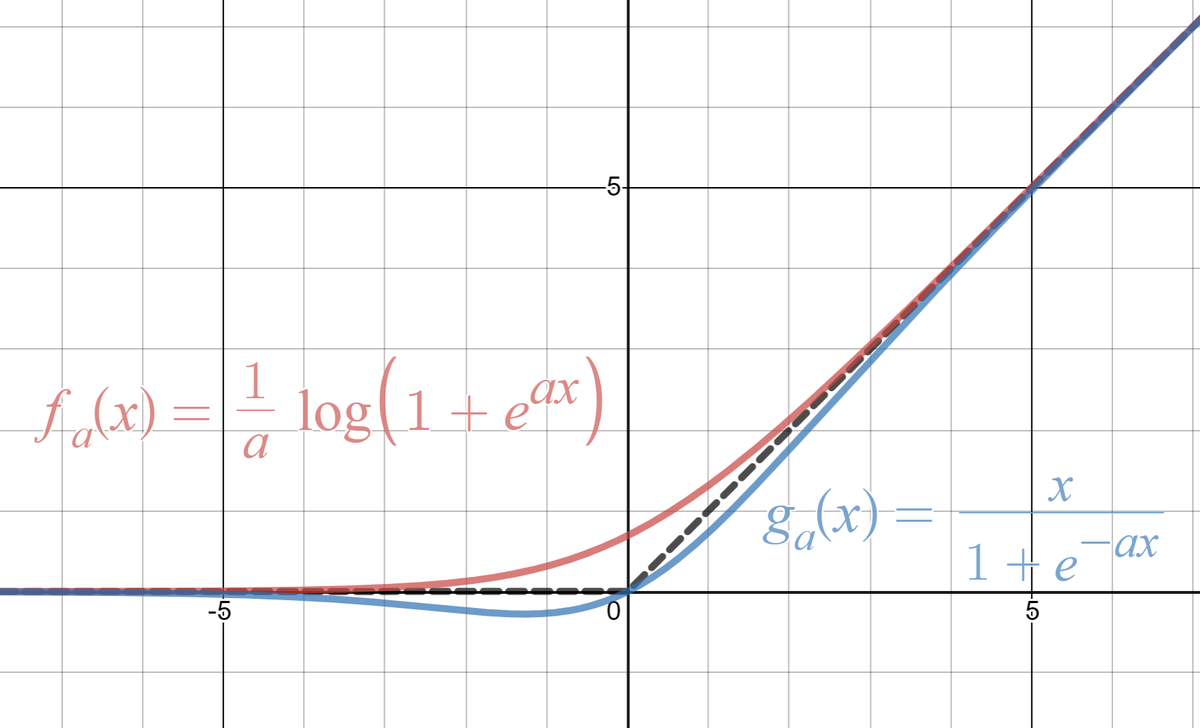
$a=1$ のとき， $f_1(x)$ ， $g_1(x)$ はそれぞれSoftplus関数，Swish関数に一致しています。さらに、 $a>0$ を大きくしていくと関数列 $(f_a)_{a>0}$ ， $(g_a)_{a>0}$ が関数 $\varphi$ に収束していく様子が観察できます。
f:id:corollary2525:20200719175836g:plain

これが得られれば、「なめらかな絶対値」まであと一歩です。

Step3 「＿／」+「＼＿」=「＼／」

あとは「絶対値の負の部分の関数」さえ得られれば、「絶対値の正の部分の関数」を足し合わせて「なめらかな絶対値」を得ることができます。「絶対値の負の部分の関数」は「絶対値の正の部分の関数」を $y$ 軸に関して対称な関数を考えればよいので、それぞれ $f_{a}(-x)$ ， $g_{a}(-x)$ で与えられますね。

ということで「なめらかな絶対値」が2つ作れました。

\begin{align*}
\lvert x\rvert_{f_a}&:=f_{a}(x)+f_{a}(-x)\\
&=\frac{1}{a}\log\big((1+e^{a x})(1+e^{-a x})\big),\\
\lvert x\rvert_{g_a}&:=g_{a}(x)+g_a(-x)\\
&=\frac{xe^{a x}-xe^{-a x}}{(1+e^{a x})(1+e^{-a x})}.
\end{align*}

f:id:corollary2525:20200720012548g:plain

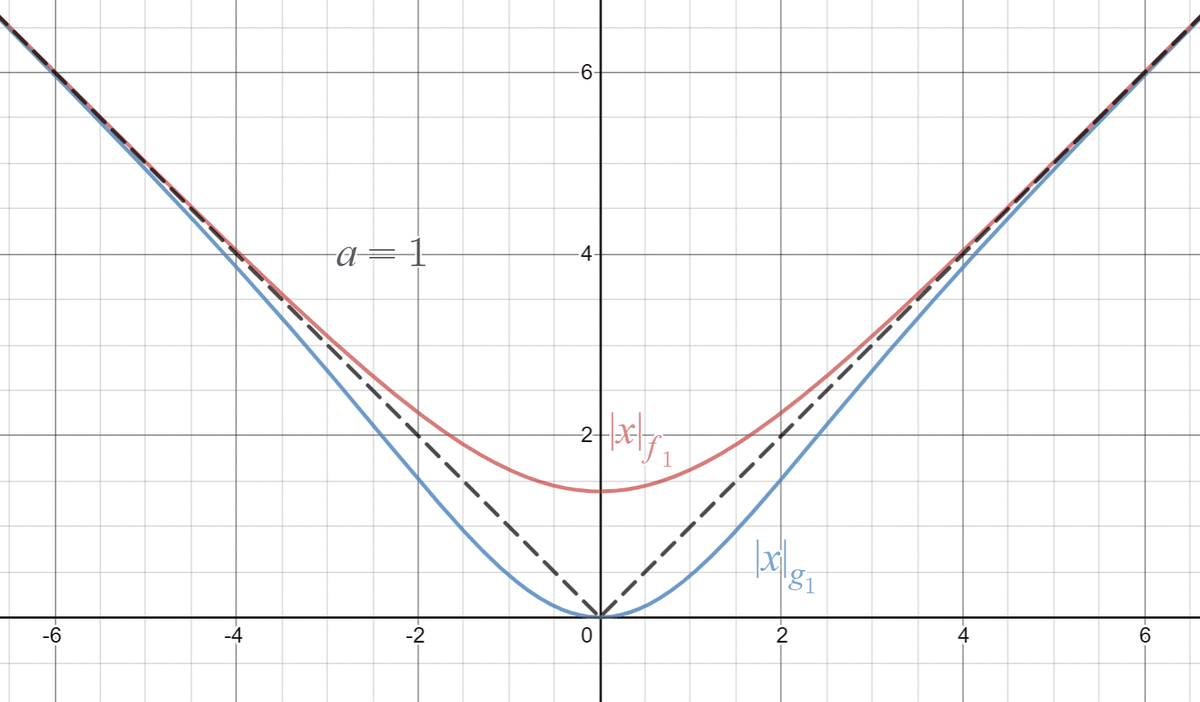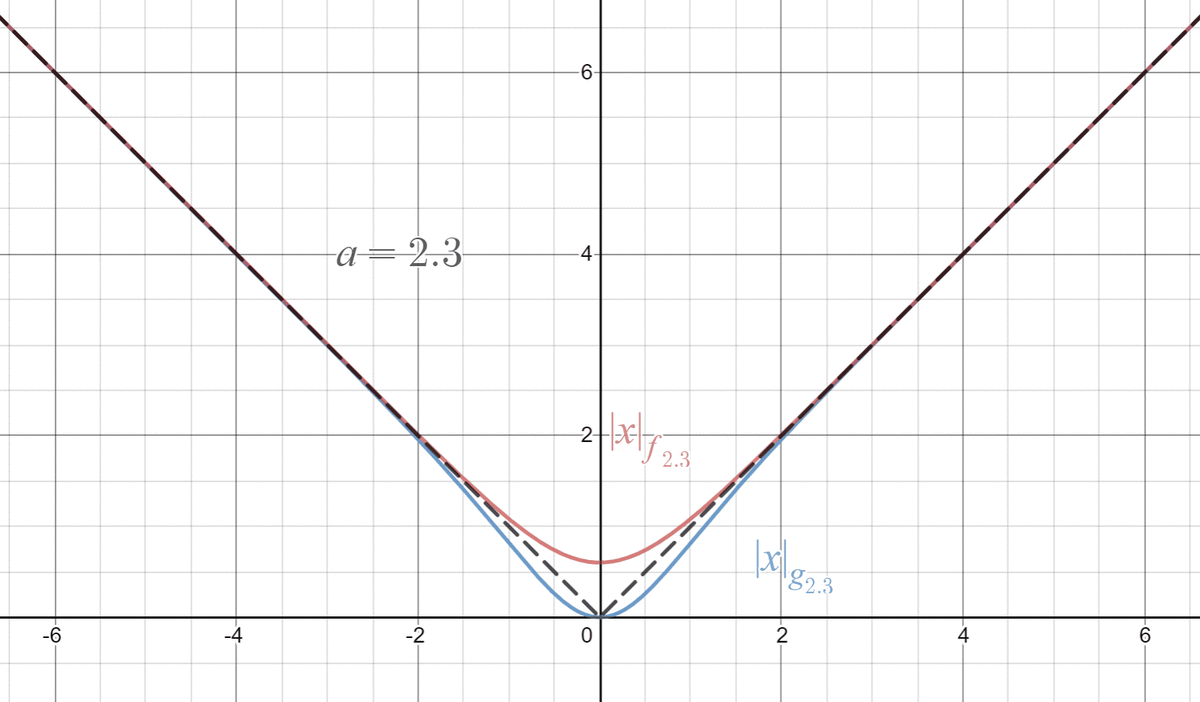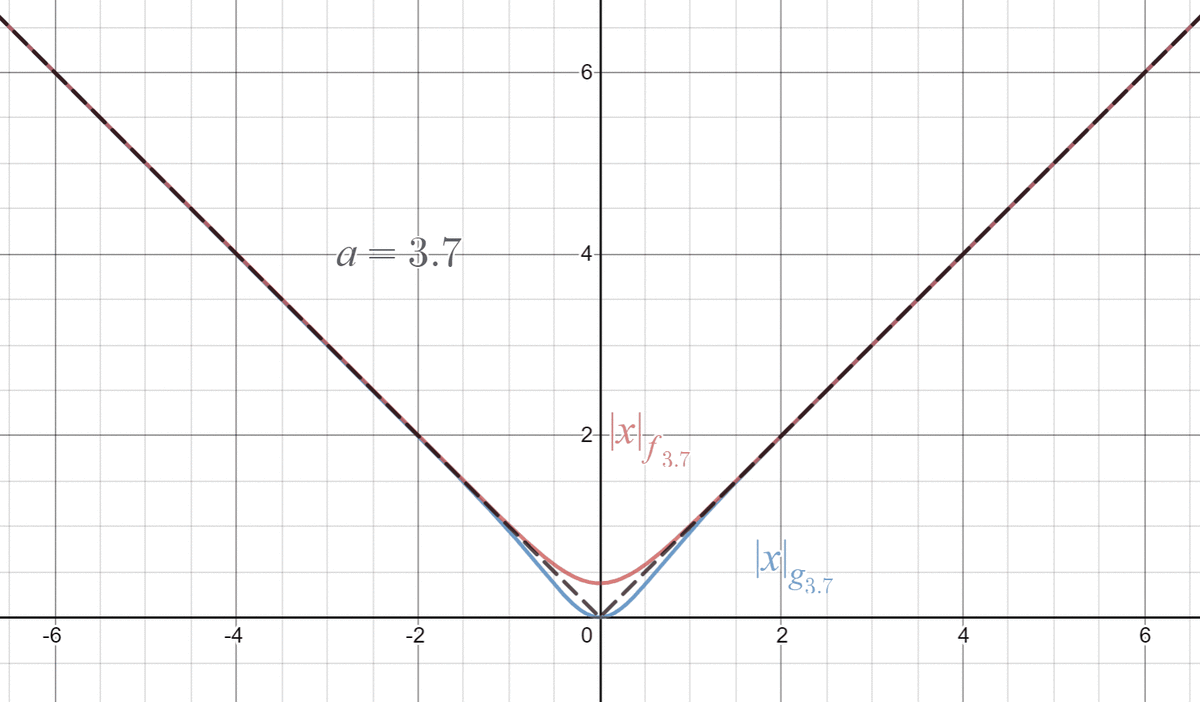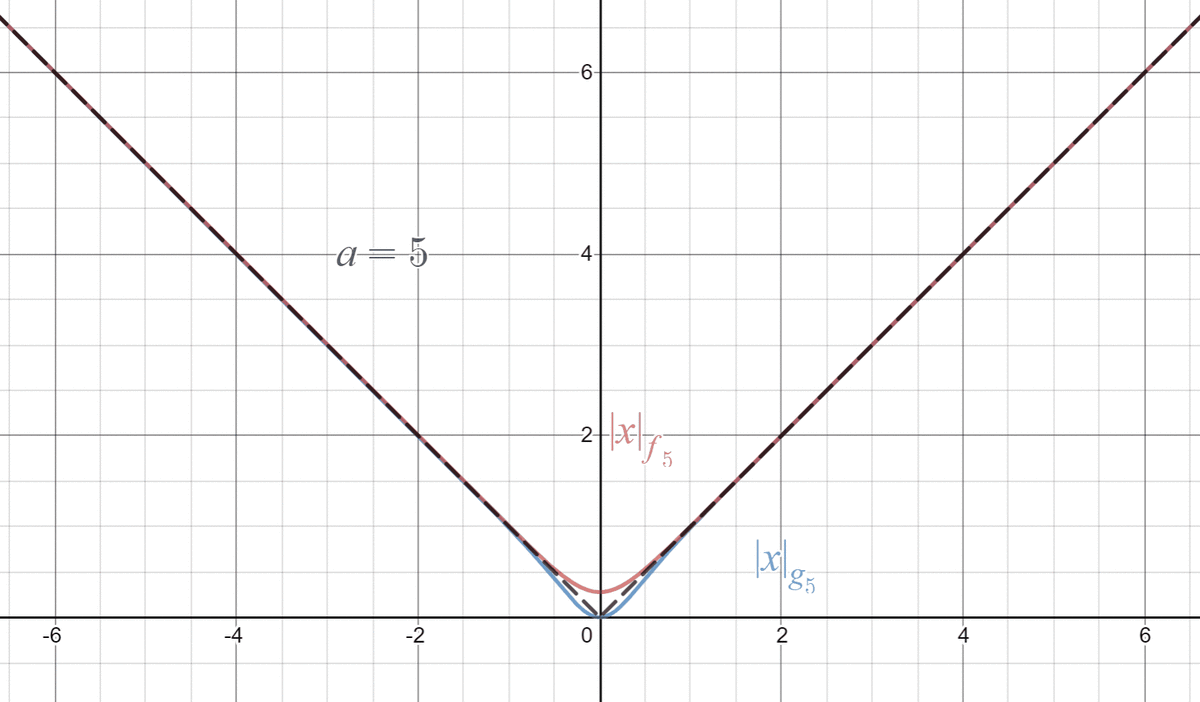
ん～なめらかですね～

Step4 Smooth maximumを作る

いよいよSmooth maximumが出来上がります。
\begin{equation*}
\max(x,y)=\dfrac{1}{2}(x+y+\lvert x-y\rvert)
\end{equation*}の絶対値を $|\cdot|_{f_a}$ ， $|\cdot|_{g_a}$ に置き換えたものを計算しましょう。

まずは $|\cdot|_{f_a}$ から：

\begin{align*}
&\dfrac{1}{2}(x+y+\lvert x-y\rvert_{f_a})\\
=&\dfrac{1}{2}\Big(x+y+\frac{1}{a}\log\big((1+e^{a(x-y)})(1+e^{-a(x-y)})\big)\Big)\\
=&\dfrac{1}{2a}\Big(\log e^{a(x+y)}+\log\big((1+e^{a(x-y)})(1+e^{a(-x+y)})\big)\Big)\\
=&\dfrac{1}{2a}\log \Big(e^{ay}(1+e^{a(x-y)})e^{ax}(1+e^{a(-x+y)})\Big)\\
=&\dfrac{1}{2a}\log(e^{ax}+e^{ay})^2\\
=&\dfrac{1}{a}\log(e^{ax}+e^{ay})
\end{align*}

お久しぶりです！ $\operatorname{LSE}_a(x,y)$ さん！

面白いことに、LogSumExp関数の $2$ 変数の場合が現れました。だからLogSumExp関数は $\max(x,y)$ を近似するんですね！ちなみに、LogSumExp - WikipediaによるとLogSumExp関数は「multivariable softplus」とも呼ばれるそうですが、確かに $\operatorname{LSE}_1(0,x)$ はSoftplus関数 $f(x)$ に一致しますし、 $\operatorname{LSE}_1(x,y)$ はSoftplus関数を多変数化したように見えます。

同じように $|\cdot|_{g_a}$ も計算してみます：

\begin{align*}
&\dfrac{1}{2}(x+y+\lvert x-y\rvert_{g_a})\\
=&\dfrac{1}{2}\Bigg(x+y+\frac{(x-y)e^{a(x-y)}-(x-y)e^{-a(x-y)}}{(1+e^{a(x-y)})(1+e^{-a(x-y)})}\Bigg)\\
=&\dfrac{1}{2}\Bigg(x+y+\frac{(x-y)e^{2ax}-(x-y)e^{2ay}}{(e^{ax}+e^{ay})(e^{ax}+e^{ay})}\Bigg)\\
=&\dfrac{1}{2}\Bigg(\frac{(x+y)(e^{2ax}+2e^{a(x+y)}+e^{2ay})}{(e^{ax}+e^{ay})^2}+\frac{(x-y)e^{2ax}-(x-y)e^{2ay}}{(e^{ax}+e^{ay})^2}\Bigg)\\
=&\dfrac{1}{2}\cdot\frac{2xe^{2ax}+2(x+y)e^{a(x+y)}+2ye^{2ay}}{(e^{ax}+e^{ay})^2}\\
=&\frac{xe^{2ax}+(x+y)e^{a(x+y)}+ye^{2ay}}{(e^{ax}+e^{ay})^2}\\
=&\frac{(xe^{ax}+ye^{ay})(e^{ax}+e^{ay})}{(e^{ax}+e^{ay})^2}\\
=&\frac{xe^{ax}+ye^{ay}}{e^{ax}+e^{ay}}
\end{align*}

これはこれは、 $S_a(x,y)$ さんではないですか！

こちらはmultivariable Swish関数の $2$ 変数の場合が現れました。こちらもLogSumExp関数と同じく、 $S_1(x,y)$ はSwish関数の多変数化とみなすことができます。私が $S_a$ を「multivariable Swish関数」と呼んでいるのはこのためです。

Smooth maximumを用いて数式お絵描き

LogSumExp関数とmultivariable Swish関数がmax関数を近似することが分かったところで、「試し描き」をしてみようと思います。

f:id:corollary2525:20200724180055p:plain — 「 $x\ge0$ と $y\ge0$ の和の境界」をなめらかに近似

f:id:corollary2525:20200724204203p:plain — 「 $y\le0$ と単位円の内側の領域の和の境界」をなめらかに近似

f:id:corollary2525:20200724201432g:plain — 2つの円をなめらかにつなぐ

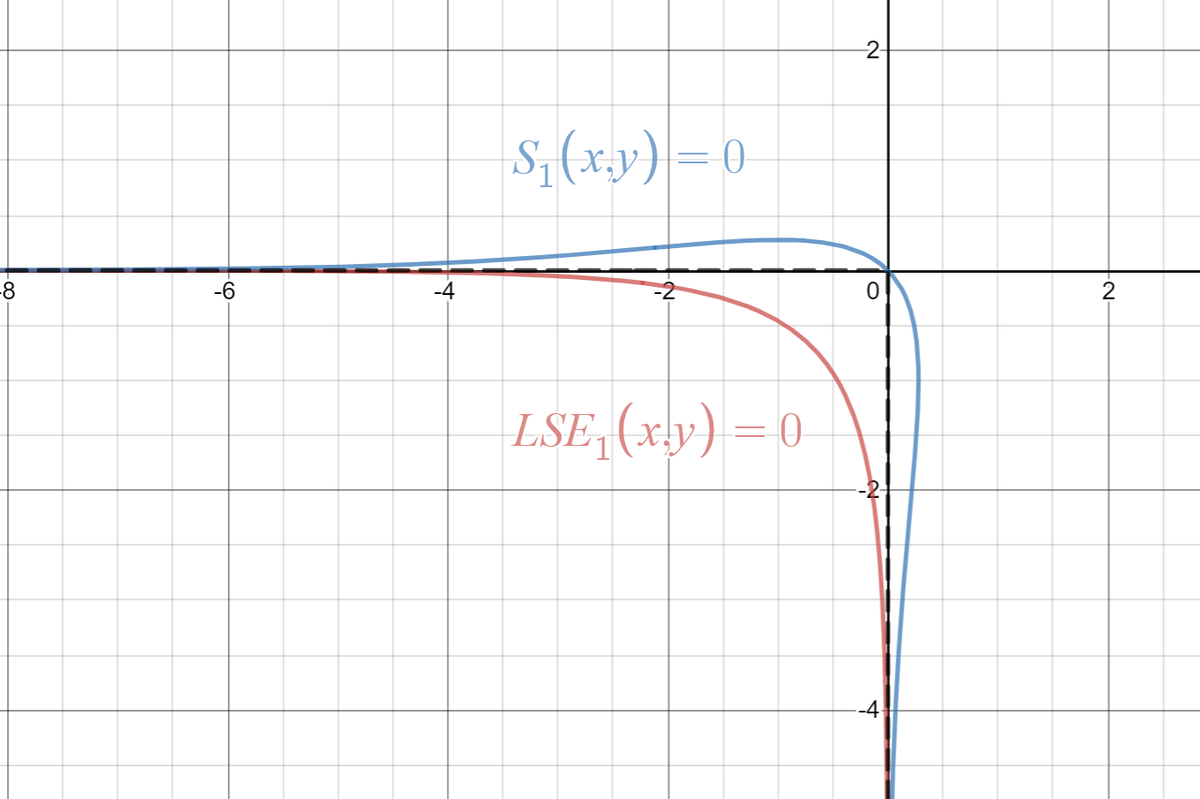
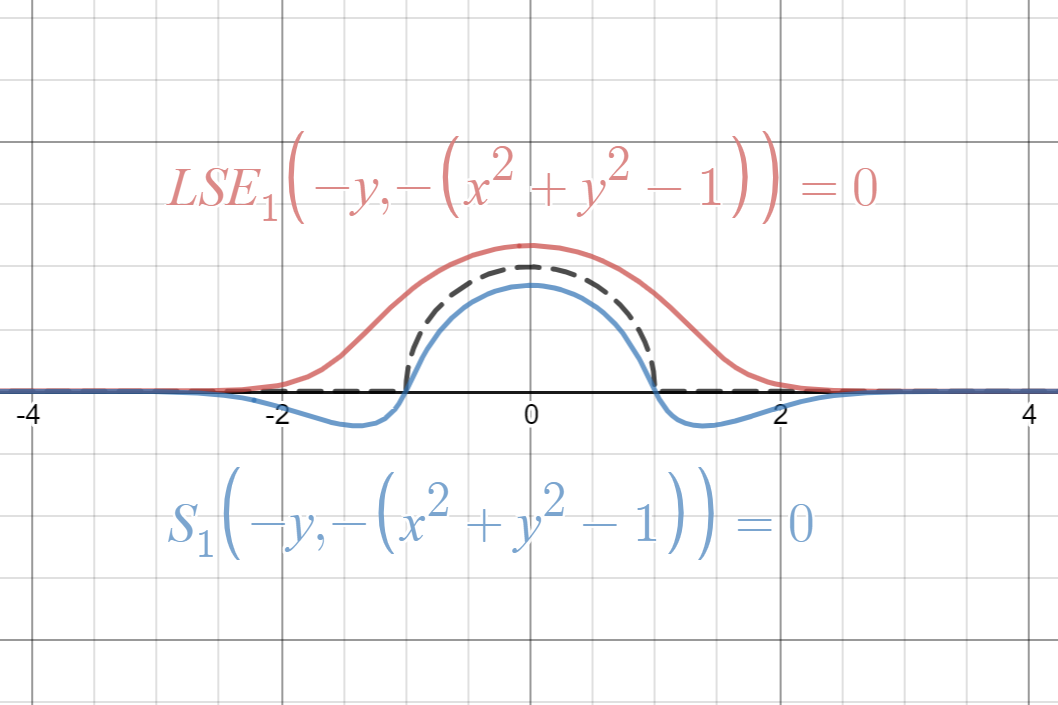
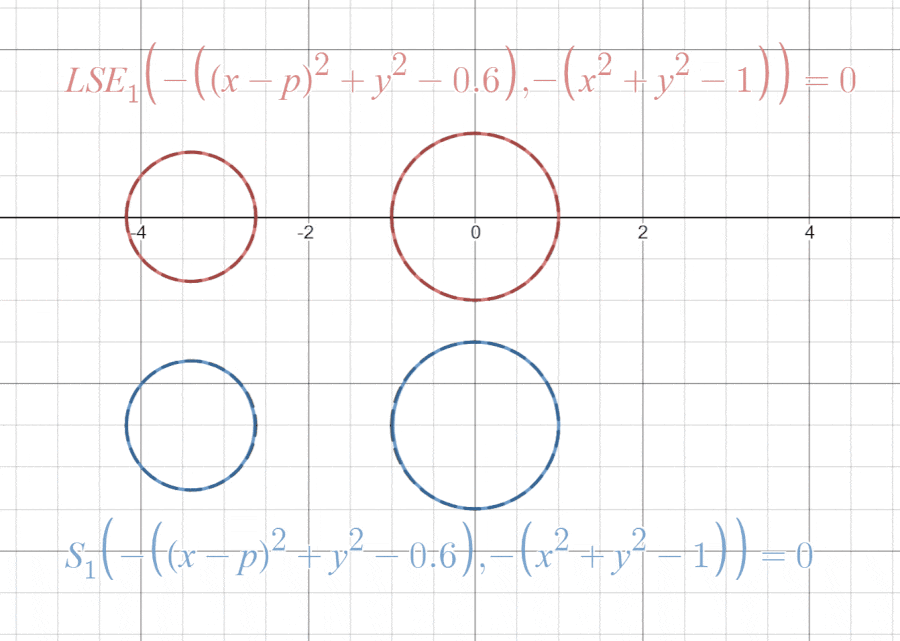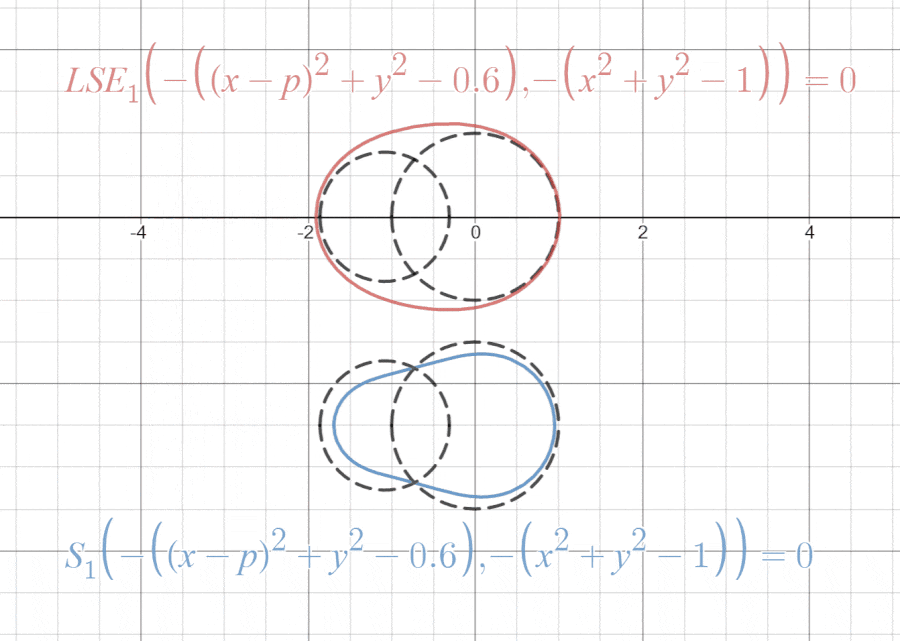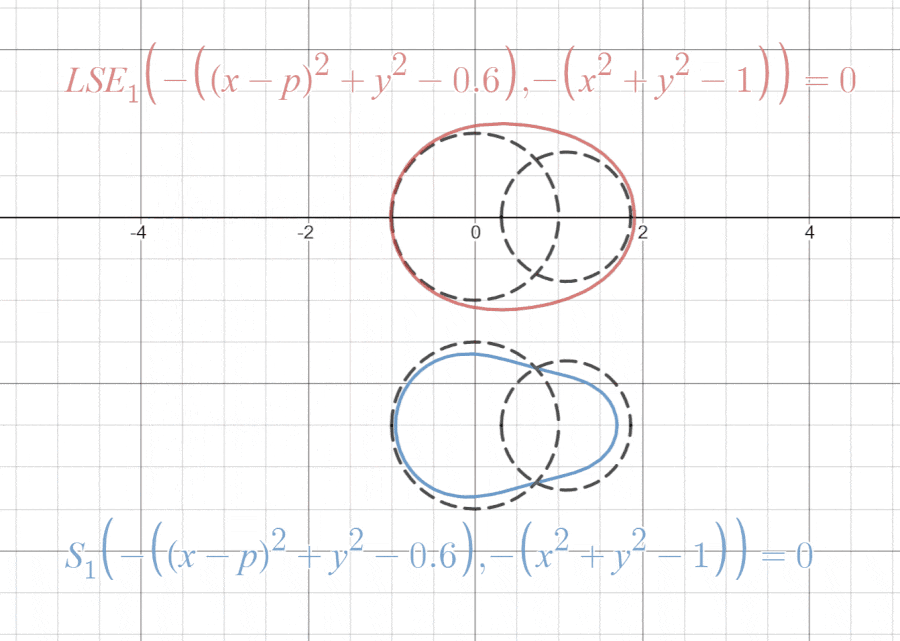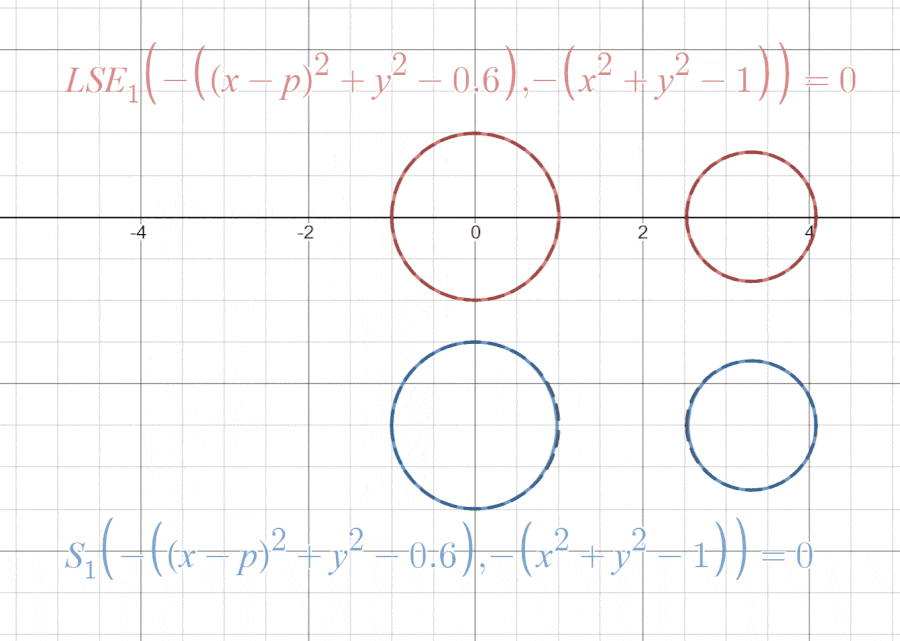
これらの「試し描き」は以下のリンクで見ることができます。
Smooth maximum
試し描きでは $a=1$ で固定しましたが、ぜひ $a$ の値を変えて遊んでみてください（ $a<0$ にすると…？）。

気づいたことをいくつか挙げると、LogSumExp関数の方は領域の外側から近似しており、multivariable Swish関数の方は領域の内側から近似しています。これはSoftplus関数が $\max(0,x)$ を上から近似し、Swish関数は下から近似していたのを思い出せば納得がいくと思います。

また、multivariable Swish関数の方は曲線の接続の前後で若干反発しているように見えますが、Swish関数のグラフは原点の前後でマイナスの方に膨らんでいたので、これが反発しているように見える要因だと考えることができます。

どちらの関数を使うかは皆さまの判断にお任せしますが、個人的にLogSumExp関数の方が無難かなと思います。

以下ではSmooth maximumを用いた数式お絵かきの例をご紹介します。

マシュマロン

小学生のときの遊戯王最強カード「マシュマロン」を数式で描きました。ついでに首を動かしてみたらウザいぞ遊戯！ pic.twitter.com/A8j2O2EtAs
— コロちゃんぬ (@corollary2525) 2020年7月22日

Smooth maximumで描いてみたいものと言えばマシュマロンですよね（？）マシュマロンの体は「試し描き」の「2つの円をなめらかにつなぐ」技術を応用しています。頭の部分を表す式を動かしてあげれば、それに応じて曲線も動いてくれます。

砂時計っぽいもの

f:id:corollary2525:20200725011027p:plain

（マシュマロンと比べると地味ですが）砂時計っぽいものを作ってみました。LogSumExp関数で作るとオリフィス（砂時計のくびれた部分）が丸みを帯びてしまうので、今回は適度に伸びるmultivariable Swish関数の方を使ってみました。

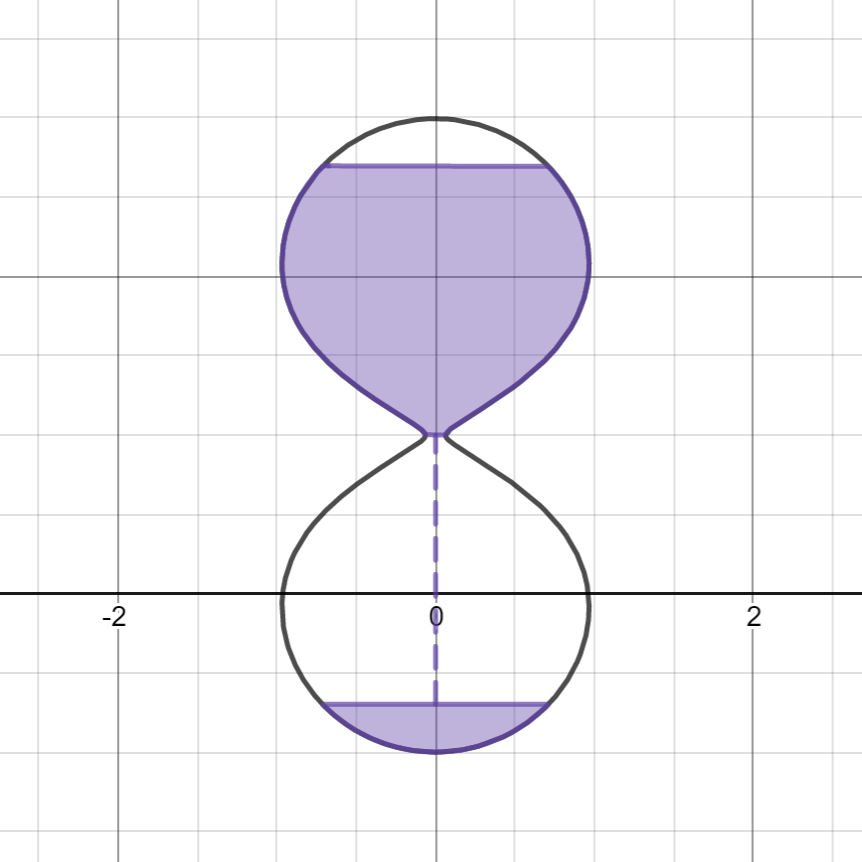
ポンデリング

#数式ポン・デ・リング（@CHARTMANq さんによる）を少しなめらかにしてみました（詳細: https://t.co/MtHEsb2J2h） pic.twitter.com/BDjICsw5m5
— コロちゃんぬ (@corollary2525) 2018年1月8日

f:id:corollary2525:20200724220142p:plain

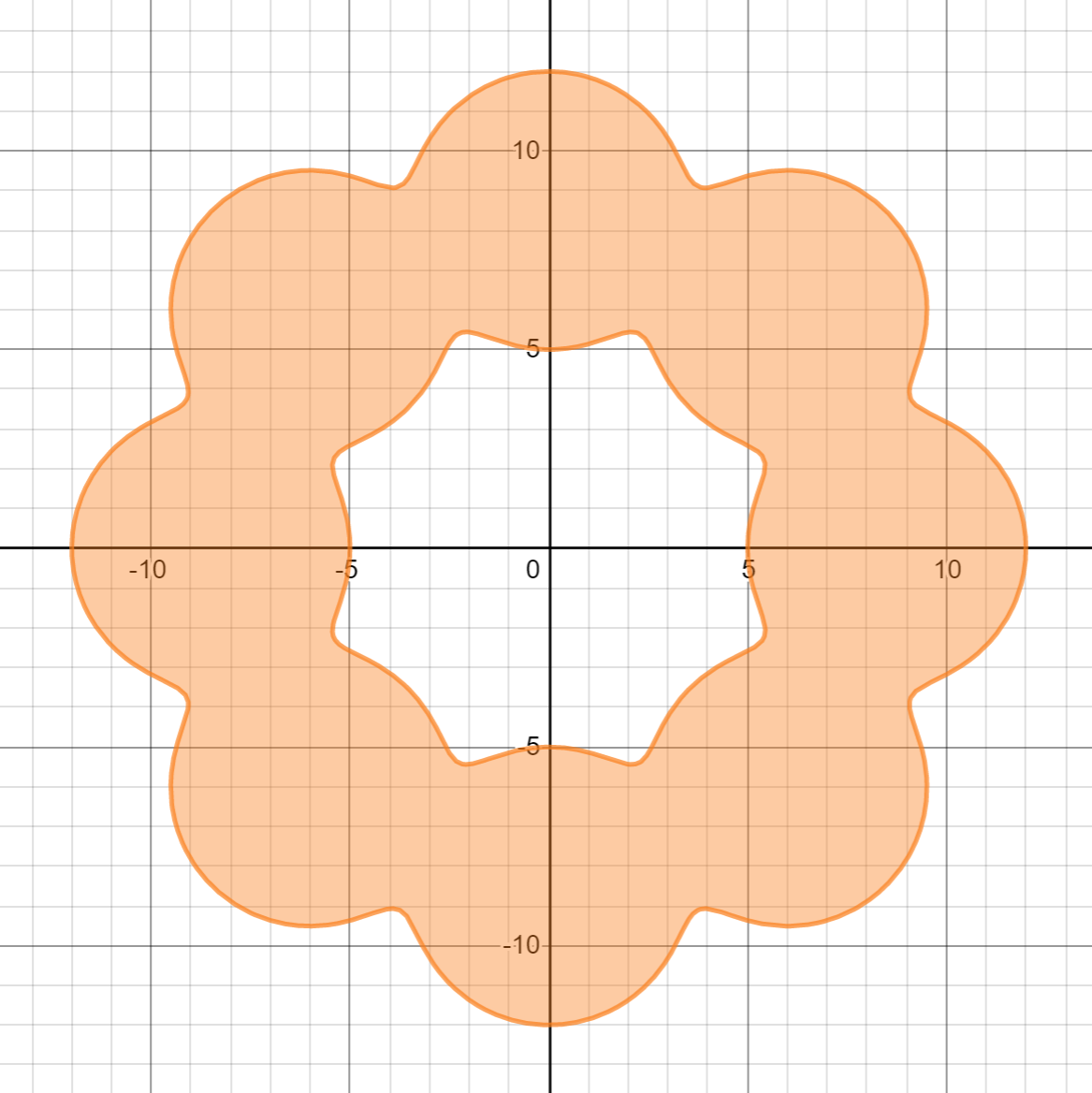
ポンデリングを表す領域をSmooth maximumを用いて作ることができます。簡単に説明すると、
\begin{equation*}
(x-p_i)^2+(y-q_i)^2-r^2=0
\end{equation*}は小さい円8個を大きく円を描くように配置したものを表すとし、左辺を $c_i(x,y)$ とおきます（ $i=1,2,\ldots,8$ ）。このとき， $-c_i(x,y)\ge0$ が円の内側の領域を表すことに注意します。これらの和集合をなめらかにつなぎたいので、

\begin{equation*}
\frac{1}{a}\log(e^{-ac_1(x,y)}+\cdots+e^{-ac_8(x,y)})\ge0
\end{equation*}

とおいて定数 $a>0$ を調整すればポンデリングの式を作ることができます。もう少し式変形をして
\begin{equation*}
e^{-ac_1(x,y)}+\cdots+e^{-ac_8(x,y)}\ge1
\end{equation*}としても良いかもしれません。

また、指数の計算のoverflow，underflowを気にするなら $m(x,y):=\displaystyle\max_{1\le i\le8}\{-c_i(x,y)\}$ とおいて

\begin{equation*}
m(x,y)+\frac{1}{a}\log(e^{a(-c_1(x,y)-m(x,y))}+\cdots+e^{a(-c_8(x,y)-m(x,y))})\ge0
\end{equation*}

あるいは

\begin{equation*}
e^{a(-c_1(x,y)-m(x,y))}+\cdots+e^{a(-c_8(x,y)-m(x,y))}\ge e^{-am(x,y)}
\end{equation*}

とするとよいと思います。

a→∞のとき一様にLSE_a→max

お待たせしました。ここからは関数列 $(\operatorname{LSE}_a)_{a > 0}$ ， $(S_a)_{a > 0}$ が $\max$ に収束することを証明します。必要であればご覧ください。

Smooth maximumの定義を振り返ると、関数列がどのくらいなめらかなのか、どのような収束を考えているのかについては明確にされていないようです。

微分可能性については少なくとも1回、欲を言えば無限回微分可能であればよいでしょう。今回紹介した $\operatorname{LSE}_a$ および $S_a$ は明らかに無限回微分可能です。

収束性については

max関数の定義域及び値域は非有界
max関数は連続であるが微分不可能な点が存在する

の2点を考慮すると、一様収束まで言えれば上出来だと思います。

ここで、各点収束と一様収束の定義を復習します。

定義

$A\subset\mathbb{R}^N$ とし， $f_n:A\to\mathbb{R}$ $(n\in\mathbb{N})$ ， $f:A\to\mathbb{R}$ とする．

$(f_n)_{n\in\mathbb{N}}$ は $f$ に $A$ 上で各点収束するとは，任意の $x\in A$ について $f_n(x)\longrightarrow f(x)\;\;(n\to\infty)$ となることを言う．
$(f_n)_{n\in\mathbb{N}}$ は $f$ に $A$ 上で一様収束するとは
\begin{equation*}\sup_{x\in A}\lvert f_n(x) - f(x)\lvert\longrightarrow 0\;\;(n\to\infty)\end{equation*}
が成り立つことを言う．

補足　各点収束は、それぞれの点 $x\in A$ に対して

\begin{equation*}\lvert f_n(x) - f(x)\lvert\longrightarrow 0\;\;(n\to\infty)\end{equation*}

となることと同値ですが、一様収束の方は先に $\lvert f_n(x) - f(x)\lvert$ の $x\in A$ に関する上限をとり、その上限が $n\to\infty$ のとき $0$ に収束することを言っています。各点収束では $\displaystyle\sup_{x\in A}\lvert f_n(x) - f(x)\lvert$ が存在するとは限らなかったり、存在したとしても $n\to\infty$ のとき $0$ に収束するかどうかは一般に分からなかったりするので、一様収束の方がより強い意味で収束することを意味します。

この記事では $n\in\mathbb{N}$ ではなく $a>0$ を使ってきたのでそのまま $a>0$ を使います。

それでは $(\operatorname{LSE}_a)_{a > 0}$ の収束について考えます。

命題1

$a>0$ とする． $\operatorname{LSE}_a$ および $\max$ は $N$ 変数関数とする．このとき， $(\operatorname{LSE}_a)_{a > 0}$ は $\max$ に $\mathbb{R}^N$ 上一様収束する．

注意　 $\operatorname{LSE}_a$ ， $\max$ はどちらも非有界なので $L^{\infty}(\mathbb{R}^N)$ での収束を意味する訳ではありません。

証明
$x=(x_1, x_2, \ldots, x_N)\in\mathbb{R}^N$ を任意にとる．このとき

\begin{align*}
\max(x_1, x_2, \ldots, x_N)
&=\frac{1}{a}\log e^{a\max(x_1, x_2, \ldots, x_N)}\\
&\le\frac{1}{a}\log\left(\sum_{i=1}^N e^{ax_i}\right)\\
&=\operatorname{L\text{SE}}_{a}(x_1, x_2, \ldots, x_N)
\end{align*}

なので

\begin{equation}
0\le\operatorname{L\text{SE}}_{a}(x)-\max(x).\label{L1}
\end{equation}

また

\begin{align*}
\operatorname{L\text{SE}}_{a}(x_1, x_2, \ldots, x_N)
&=\frac{1}{a}\log\left(\sum_{i=1}^N e^{a x_i}\right)\\
&\le\frac{1}{a}\log\left(\sum_{i=1}^N e^{a\max(x_1, x_2, \ldots, x_N)}\right)\\
&=\frac{1}{a}\log\left(N e^{a\max(x_1, x_2, \ldots, x_N)}\right)\\
&=\frac{\log N}{a}+\max(x_1, x_2, \ldots, x_N)\\
\end{align*}

であるから

\begin{equation}
\operatorname{L\text{SE}}_{a}(x)-\max(x)\le\frac{\log N}{a}.\label{L2}
\end{equation}

\eqref{L1}，\eqref{L2}より $x\in\mathbb{R}^N$ に関する上限をとると

\begin{align*}
\sup_{x\in\mathbb{R}^N}\lvert\operatorname{L\text{SE}}_{a}(x)-\max(x)\rvert
&\le\frac{\log N}{a}\\
&\longrightarrow 0\;\;(a\to\infty)
\end{align*}

となるので， $(\operatorname{LSE}_{a})_{a > 0}$ は $\max$ に $\mathbb{R}^N$ 上一様収束する．■

補足　 $\operatorname{LSE}_{a}$ は $a<0$ の場合にも定義されますが、 $a\to-\infty$ のとき $(\operatorname{LSE}_{a})_{a < 0}$ は $\min$ に $\mathbb{R}^N$ 上一様収束します．証明は $a < 0$ であることと不等号の向きに注意すれば命題1と同様です．

a→∞のとき一様にS_a→max？

同じようにして $(S_a)_{a > 0}$ が $\max$ に一様収束することを証明したかったのですが、 $N=2$ の場合しか証明できませんでした。各点収束することは $N$ 変数で証明できます。

命題2

$a>0$ とする． $S_a$ および $\max$ は $N$ 変数関数とする．このとき， $(S_a)_{a > 0}$ は $\max$ に $\mathbb{R}^N$ 上各点収束する．

証明
$x=(x_1, x_2, \ldots, x_N)\in\mathbb{R}^N$ を任意にとる． $x_i=\max(x)$ をみたす $x_i$ の個数を $k$ とおくと $k\neq 0$ であるから

\begin{align*}
S_a(x)&=\dfrac{\sum_{i=1}^N x_i e^{a x_i}}{\sum_{i=1}^N e^{a x_i}}\\
&=\dfrac{k\max(x)+\sum_{x_i< \max(x)} x_i e^{a (x_i-\max(x))}}{k+\sum_{x_i< \max(x)} e^{a (x_i-\max(x))}}\\
&\longrightarrow \dfrac{k\max(x)}{k}=\max(x)\;\;(a\to\infty).
\end{align*}

よって， $(S_a)_{a > 0}$ は $\max$ に $\mathbb{R}^N$ 上各点収束する．■

補足　 $S_{a}$ は $a<0$ の場合にも定義されますが、お察しのとおり $a\to-\infty$ のとき $(S_{a})_{a < 0}$ は $\min$ に $\mathbb{R}^N$ 上各点収束します．証明は $a < 0$ と $(x_i - \min(x) )$ の符号に注意すれば命題2と同様です．ちなみに $a=0$ のとき， $S_0(x_1, x_2, \ldots, x_N)$ は相加平均 $\displaystyle\frac{1}{N}\sum_{i=1}^N x_i$ に一致します。面白いですね。

次に $N=2$ のとき $(S_a)_{a > 0}$ が $\max$ に一様収束することを示します。

命題3

$g_{a}(x)=\dfrac{x}{1+e^{-a x}}$ ， $\lvert x\rvert_{g_a}=g_{a}(x)+g_a(-x)$ とおく（ $a > 0$ ）．

$(g_{a})_{a > 0}$ は $\max(0,\cdot)$ に $\mathbb{R}$ 上一様収束する．
$(|\cdot|_{g_a})_{a > 0}$ は $|\cdot|$ に $\mathbb{R}$ 上一様収束する．
$(S_a(\cdot,\cdot) )_{a > 0}$ は $\max(\cdot,\cdot)$ に $\mathbb{R}^2$ 上一様収束する．

証明
$x\le0$ のときは $g_a(x)\le0$ ， $x > 0$ のときは $g_a(x) < x$ であるから，任意の $x\in\mathbb{R}$ に対して $g_a(x)\le\max(0,x)$ ．また

\begin{align*}
\max(0,-x) - g_a(-x)
&=\max(0,-x) + \frac{x}{1+e^{ax}}\\
&=\max(0,-x) + x - \frac{xe^{ax}}{1+e^{ax}}\\
&=\max(x,0) - \frac{x}{1+e^{-ax}}\\
&=\max(0,x) - g_a(x)
\end{align*}

なので $\max(0,\cdot) - g_a$ は偶関数である．したがって

\begin{align*}
\sup_{x\in\mathbb{R}}|g_a(x) - \max(0,x)|
&=\sup_{x\ge0} (\max(0,x) - g_a(x))\\
&=\sup_{x\ge0} \left(x - \frac{x}{1+e^{-ax}}\right)\\
&=\frac{1}{a}\sup_{x\ge0} \frac{ax}{1+e^{ax}}\\
&\le\frac{1}{a}\sup_{x\ge0} \frac{ax}{2+ax}\\
&\le\frac{1}{a}\\
&\longrightarrow 0\;\;(a\to\infty).
\end{align*}

よって $a\to\infty$ のとき $(g_{a})_{a > 0}$ は $\max(0,\cdot)$ に一様収束する．

また、

\begin{align*}
\sup_{x\in\mathbb{R}}|\lvert x\rvert - \lvert x\rvert_{g_a}|
&=\sup_{x\in\mathbb{R}}|\max(x,-x) - g_{a}(x) - g_a(-x)|\\
&=\sup_{x\in\mathbb{R}}|\max(x,0)+\max(0,-x) - g_{a}(x) - g_a(-x)|\\
&\le\sup_{x\in\mathbb{R}}|\max(0,x)- g_{a}(x)| + \sup_{x\in\mathbb{R}}|\max(0,-x) - g_a(-x)|\\
&\longrightarrow 0\;\;(a\to\infty)
\end{align*}

であるから $(|\cdot|_{g_a})_{a > 0}$ は $|\cdot|$ に一様収束する．

したがって

\begin{align*}
\sup_{(x,y)\in\mathbb{R}^2}|\max(x,y) - S_a(x,y)|
&=\frac{1}{2}\sup_{(x,y)\in\mathbb{R}^2}| |x-y| - g_a(x-y) - g_a(y-x)|\\
&=\frac{1}{2}\sup_{(x,y)\in\mathbb{R}^2}| |x-y| - |x-y|_{g_a}|\\
&=\frac{1}{2}\sup_{x\in\mathbb{R}}| |x| - |x|_{g_a}|\\
&\longrightarrow 0\;\;(a\to\infty).
\end{align*}

これは $(S_a(\cdot,\cdot) )_{a > 0}$ が $\max(\cdot,\cdot)$ に $\mathbb{R}^2$ 上一様収束することを示している．■

$3$ 変数以上の場合でも $(S_a)_{a > 0}$ は $\max$ に一様収束しそうなんですけどね～。何か進捗があったら追記します。

メモ　 $N=2$ で一様収束することを証明できた要因は $\max(x,y)$ の絶対値を用いた表示が $S_a(x,y)$ の $|\cdot|_{g_a}$ を用いた表示と相性がよかったことと、 $\max(0,\cdot) - g_a$ が対称的なグラフだったので $\sup$ の範囲を狭めることができたことかな。 $\max(x,y,z)$ を絶対値で表示しようとすると複雑だから諦めた。あと、
\begin{align*}
\max(x,y,z)&=\max(\max(x,y),z)\\
\operatorname{L\text{SE}}_a(x,y,z)&=\operatorname{L\text{SE}}_a(\operatorname{L\text{SE}}_a(x,y),z)
\end{align*}が成り立つから $\operatorname{LSE}_a$ の方は $N$ に関する帰納法が回ることが分かったけど、 $S_a(S_a(x,y),z)$ を計算して整理すると

$S_a(S_a(x,y),z)=\frac{xe^{ax}+ye^{ay}+ze^{az}e^{a(\operatorname{LSE}_a(x,y)-S_a(x,y))}}{e^{ax}+e^{ay}+e^{az}e^{a(\operatorname{LSE}_a(x,y)-S_a(x,y))}}$

という変なゴミが出てきてしもた。そんなに悪さをしないゴミではあるけれど、分子分母両方にあると面倒くさいな。うーん、どうしよっかな～