n=±1±2±...±Nと表せる最小のNに関する予想

「1，2，3，4を足したり引いたりして，2をつくってみましょう」
「1，2，3を足したり引いたりして，2をつくってみましょう」
「1，2を足したり引いたりして，2をつくることができるでしょうか？」

簡単な足し算引き算の問題ですがいかがでしょうか？
さらに話を発展させて、3をつくれたりするでしょうか？
1，2，3，4，5を足したり引いたりして，12をつくれるでしょうか？

そんな、1から連続する自然数を足し引きする話です。

動機
n=±1±2±...±Nと表せる最小のN
OEISと謎の予想
予想が言っている意味
証明に挑戦
あとがきと研究課題

動機

きっかけは次の盛田みずすましさんのツイートです。

A_N:={Σ_{n=1}^{N}n(-1)^a_n|(a_n)∈{0,1}^N}

A:=∪_{N=1}^{∞}A_N

としたとき、A=ℤ？
— 盛田みずすまし (@nosiika) 2020年5月26日

やさしい言葉で言い換えると、「1から連続する有限個の自然数を足し引きして、すべての整数をつくることができるか？」という問題です。厳密に言うと次のようになります（都合により表記が少し異なる部分がありますが全く同じ問題です）。

問題（盛田みずすまし, 2020）

正の整数 $N$ に対して

\begin{equation*}
A_N :=\left\{\sum_{n=1}^N (-1)^{e_n}n\;\middle|\; e_n\in\mathbb{N}\;(n=1,2,\ldots,N) \right\}
\end{equation*}

と定め，
\begin{equation*}
A :=\bigcup_{N=1}^{\infty}A_N
\end{equation*}とおく．このとき， $A=\mathbb{Z}$ か？

$e_n$ は自然数なので， $n=1,2,\ldots,N$ に対して $(-1)^{e_n}$ は1か-1のどちらかです。よって
\begin{equation*}
\sum_{n=1}^N (-1)^{e_n}n=\pm1\pm2\pm\cdots\pm N
\end{equation*}と表すこともできます。つまり， $A_N$ は1から連続するN個の自然数を足し引きしてできる整数の集合を表します。具体的に $A_1$ から $A_4$ まで求めてみると

\begin{align*}
A_1 &=\{1,-1\},\\
A_2 &=\{\pm1\pm2\}=\{3,1,-1,-3\},\\
A_3 &=\{\pm1\pm2\pm3\}=\{6,4,2,0,-2,-4,-6\},\\
A_4 &=\{\pm1\pm2\pm3\pm4\}=\{10,8,6,4,2,0,-2,-4,-6,-8,-10\}
\end{align*}

といった具合になります。ただし
\begin{alignat*}{2}
2&=& 1+2+3-4\\
&=&-1+2-3+4
\end{alignat*}のように、1つの数に対して複数の表示がありえるので、符号の決め方の総数である $2^N$ 通りが $A_N$ の元の個数に等しくなるとは限りません。

それでは盛田みずすましさんの問題を考えてみましょう。自然数の列1，2，3，4，…は隣り合う数の差が1であることに注目すると

\begin{align*}
-1+2=1,\quad -3+4=1,\quad -5+6=1
\end{align*}

のように1をいくらでも作れます。したがって，正の整数 $n$ に対しては1から2nまでの自然数を用意すれば

\begin{align*}
\sum_{k=1}^{2n}(-1)^k k &=\underbrace{-1+2}_{+1}\underbrace{-3+4}_{+1}-\cdots\underbrace{-(2n-1)+2n}_{+1}\\
&=n
\end{align*}

と表すことができます。負の整数 $-n$ （ $n >0$ ）に対しては

\begin{align*}
\sum_{k=1}^{2n}(-1)^{k+1} k &=\underbrace{1-2}_{-1}+\underbrace{3-4}_{-1}+\cdots+\underbrace{(2n-1)-2n}_{-1}\\
&=-n
\end{align*}

とすればよいですね。最後に0が残っていますが、
\begin{equation*}
1+2-3=0
\end{equation*}なので大丈夫です。以上より、盛田みずすましさんの問題を解くことができました。

n=±1±2±...±Nと表せる最小のN

話はこれで終わるはずはなく、2020年5月29日の数学デーの参加者でこの話を発展させて色々議論しました。
sugakuday.fanbox.cc
その中でも私は

$n=\pm1\pm2\pm\cdots\pm N$ と表せる最小の $N$

についての話が面白かったです。

先ほど証明したように、正の整数 $n$ に対しては $1$ から $2n$ までの自然数を用意すれば

\begin{equation*}
n=-1+2-3+4-\cdots-(2n-1)+2n
\end{equation*}

と表すことができます。例えば $n=2$ であれば1から4までの自然数を用意して
\begin{equation*}
2=-1+2-3+4
\end{equation*}と表すことができます。しかし、
\begin{equation*}
2=1-2+3
\end{equation*}なので、より少ない自然数で表現することもできます。また、1と2の足し引きで2を作ることはできないので、2を作るには最低で1から3までの自然数が必要であることが分かりました。

そこで、正の整数 $n$ に対して $n=\pm1\pm2\pm\cdots\pm N$ と表せる最小の $N$ を $a_n$ と表すことにします。正確に記述すると次のようになります。

定義

正の整数 $N$ に対して

\begin{equation*}
A_N :=\left\{\sum_{n=1}^N (-1)^{e_n}n\;\middle|\; e_n\in\mathbb{N}\;(n=1,2,\ldots,N) \right\}
\end{equation*}

とおいたとき，数列 $(a_n)_n$ を
\begin{equation*}
a_n:=\min\{N\in\mathbb{N}\mid n\in A_N\}
\end{equation*}によって定義する．

それでは $a_n$ の値を具体的に求めてみましょう。 $n=2$ のときは1から3までの自然数が必要だったので $a_2=3$ となります。さらに $n=15$ までの自然数については
\begin{alignat*}{2}
1&= &1&\\
2&=&1&-2+3\\
3&=&1&+2\\
4&=&-1&+2+3\\
5&=&-1&+2+3-4+5\\
6&=&1&+2+3\\
7&=&1&+2+3-4+5\\
8&=&-1&+2+3+4\\
9&=&1&+2-3+4+5\\
10&=&1&+2+3+4\\
11&=&1&-2+3+4+5\\
12&=&1&-2+3+4+5-6+7\\
13&=&-1&+2+3+4+5\\
14&=&-1&+2+3+4+5-6+7\\
15&=&1&+2+3+4+5
\end{alignat*}のように表すことができ、それぞれこれより少ない数では表示できません（ただし $5=1+2+3+4-5$ などの表示もできるので、最小だったとしても表示は一通りとは限りません）。

したがって， $a_1=1$ ， $a_2=3$ ， $a_3=2$ ， $a_4=3$ ， $a_5=5$ ， $a_6=3$ ， $a_7=5$ ， $a_8=4$ ， $a_9=5$ ， $a_{10}=4$ ，…が求まります。

1, 3, 2, 3, 5, 3, 5, 4, 5, 4, 5, 7, 5, 7, 5

なんだこれ？増えたり減ったり、たまに2連続で増えたり、それでいて全体的に緩やかに増加しているように見えます。

そんなときは、「あいつ」の力に頼ってみましょうか…！？

OEISと謎の予想

2020年5月29日の数学デーの参加者の一人がこの数列をオンライン整数列大辞典（OEIS）で調べてくれました。
oeis.org

OEISに数列をいくつか並べて検索すると、サイトに登録されている数列をサジェストしてくれます。私もこのサイトに
1, 3, 2, 3, 5, 3, 5, 4, 5, 4, 5, 7, 5, 7, 5
を入力して検索してみたのですが、1件ヒットしました。1件ですか…ドキドキワクワク…！

oeis.org

f:id:corollary2525:20200601034622p:plain

記事のタイトルは「Smallest positive integer k such that n = +-1+-2+-...+-k for some choice of +'s and -'s.」ですって。

お前やー！まさにお前やー！

しかもこの記事の投稿は2008年。割と最近。

すでに先人たちが考え尽くしていたんですね。だってほら、もうFOMULAの欄がしっかり埋まって…

f:id:corollary2525:20200606013250p:plain

んん～～～？？？
こ、Conjecture…だとぉ！？

少なくともこのサイト内では未解決だったのか！

とりあえず自分なりに体裁を整えて訳してみます。

予想

自然数 $n$ に対して $T_k\le n< T_{k+1}$ となる自然数 $k$ をとる（ただし $T_k=\frac{k(k+1)}{2}$ は三角数）． $n=T_k$ であれば $a_n=k$ ， $n\neq T_k$ であれば $a_n$ は以下で与えられる:

\begin{equation*}
a_n=
\begin{cases}
k+2 & (k\text{は奇数}, n-T_k\text{は奇数})\\
k+1 & (k\text{は奇数}, n-T_k\text{は偶数})\\
k+1 & (k\text{は偶数}, n-T_k\text{は奇数})\\
k+3 & (k\text{は偶数}, n-T_k\text{は偶数})
\end{cases}
\end{equation*}

三角数とは次のように点を正三角形の形に並べたときの点の総数のことです。
f:id:corollary2525:20200604234437p:plain

$k$ 番目の三角数は $1$ から $k$ までの自然数の和に等しいので
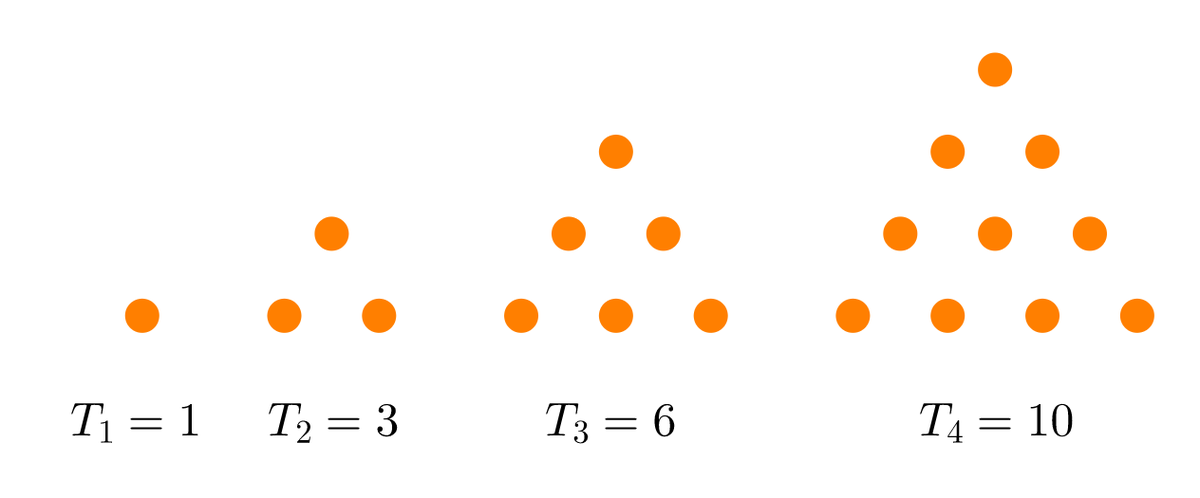
\begin{equation*}
T_k=1+2+\cdots+k=\frac{k(k+1)}{2}
\end{equation*}となります。また、漸化式を用いて
\begin{equation*}
T_{k+1}=T_k + k+1
\end{equation*}と表すことができます。

予想が言っている意味

場合分けが多くてよくわからないと思うので、この予想が何を言っているかについて解説します。まずはOEISで検索して得られた $a_1$ から $a_{83}$ までの値を次のように改行してグループ分けし、上から第1群、第2群、…と呼ぶことにします。

\begin{array}{llllllllllll}
1, &&&&&&&&&&\\
3, &2, &&&&&&&&&&\\
3, &5, &3, &&&&&&&&&\\
5, &4, &5, &4, &&&&&&&&\\
5, &7, &5, &7, &5, &&&&&&&\\
7, &6, &7, &6, &7, &6, &&&&&&\\
7, &9, &7, &9, &7, &9, &7, &&&&&\\
9, &8, &9, &8, &9, &8, &9, &8, &&&&\\
9, &11, &9, &11, &9, &11, &9, &11, &9, &&&\\
11, &10, &11, &10, &11, &10, &11, &10, &11, &10, &&\\
11, &13, &11, &13, &11, &13, &11, &13, &11, &13, &11, &\\
13, &12, &13, &12, &13, &12, &13, &12, &13, &12, &13, &12, \\
13, &15, &13, &15, &13&&&&&&&
\end{array}

最後の第13群が足りてないですが後で予想をもとに埋めましょう（この時点で余裕で埋めらるんですが我慢我慢）。

$a_n$ がちょうど三角数番目のとき

最初はそれぞれのグループの最後尾に注目します。

\begin{array}{llllllllllll}
\color{red}{1}, &&&&&&&&&&\\
3, &\color{red}{2}, &&&&&&&&&&\\
3, &5, &\color{red}{3}, &&&&&&&&&\\
5, &4, &5, &\color{red}{4}, &&&&&&&&\\
5, &7, &5, &7, &\color{red}{5}, &&&&&&&\\
7, &6, &7, &6, &7, &\color{red}{6}, &&&&&&\\
7, &9, &7, &9, &7, &9, &\color{red}{7}, &&&&&\\
9, &8, &9, &8, &9, &8, &9, &\color{red}{8}, &&&&\\
9, &11, &9, &11, &9, &11, &9, &11, &\color{red}{9}, &&&\\
11, &10, &11, &10, &11, &10, &11, &10, &11, &\color{red}{10}, &&\\
11, &13, &11, &13, &11, &13, &11, &13, &11, &13, &\color{red}{11}, &\\
13, &12, &13, &12, &13, &12, &13, &12, &13, &12, &13, &\color{red}{12}, \\
13, &15, &13, &15, &13&&&&&&&
\end{array}

$a_1=1$ ， $a_3=2$ ， $a_6=3$ ，…， $a_{78}=12$ となっていますね。これは
「1番目の値は1」
「1+2=3番目の値は2」
「1+2+3=6番目の値は3」
…
「1+2+…+12=78番目の値は12」
となっているので
「 $n$ が $k$ 番目の三角数のときは $a_n=k$ である」
と予想できます。これはまさに次の赤字で記した部分を指しています。

自然数 $n$ に対して $T_k\le n< T_{k+1}$ となる自然数 $k$ をとる（ただし $T_k=\frac{k(k+1)}{2}$ は三角数）． $n=T_k$ であれば $a_n=k$ ， $n\neq T_k$ であれば $a_n$ は以下で与えられる:

この部分の証明は簡単です。というのも $k$ 番目の三角数は
\begin{equation*}
T_k=1+2+\cdots+k
\end{equation*}と表せますが， $1$ から $k-1$ 以下までの自然数の足し引きでは $T_k$ に絶対届かないので $k$ が最小です。

$a_n$ が偶数番目のグループに属するとき

次に $n$ が三角数でない場合です。まずは $k$ が奇数かつ $a_n$ は第 $k+1$ 群に属する場合（赤字の値）を考えます。

\begin{array}{llllllllllll}
1, &&&&&&&&&&\\
\color{red}{3}, &\color{blue}{2}, &&&&&&&&&&\\
3, &5, &3, &&&&&&&&&\\
\color{red}{5}, &\color{red}{4}, &\color{red}{5}, &\color{blue}{4}, &&&&&&&&\\
5, &7, &5, &7, &5, &&&&&&&\\
\color{red}{7}, &\color{red}{6}, &\color{red}{7}, &\color{red}{6}, &\color{red}{7}, &\color{blue}{6}, &&&&&&\\
7, &9, &7, &9, &7, &9, &7, &&&&&\\
\color{red}{9}, &\color{red}{8}, &\color{red}{9}, &\color{red}{8}, &\color{red}{9}, &\color{red}{8}, &\color{red}{9}, &\color{blue}{8}, &&&&\\
9, &11, &9, &11, &9, &11, &9, &11, &9, &&&\\
\color{red}{11}, &\color{red}{10}, &\color{red}{11}, &\color{red}{10}, &\color{red}{11}, &\color{red}{10}, &\color{red}{11}, &\color{red}{10}, &\color{red}{11}, &\color{blue}{10}, &&\\
11, &13, &11, &13, &11, &13, &11, &13, &11, &13, &11, &\\
\color{red}{13}, &\color{red}{12}, &\color{red}{13}, &\color{red}{12}, &\color{red}{13}, &\color{red}{12}, &\color{red}{13}, &\color{red}{12}, &\color{red}{13}, &\color{red}{12}, &\color{red}{13}, &\color{blue}{12}, \\
13, &15, &13, &15, &13&&&&&&&
\end{array}

それぞれのグループの奇数番目は最後尾の値より1大きく、偶数番目は最後尾の値と同じに見えます。最後尾の値は $\color{blue}{k+1}$ です。あとは $a_n$ が第 $k+1$ 群の何番目かが分かればいいのですが、どうなるんでしょう（すっとぼけ）。

はい、1つ前の第 $k$ 群の最後尾が $T_k$ 番目なので、 $a_n$ は第 $k+1$ 群の $n-T_k$ 番目ですよね。

したがって、 $n-T_k$ が奇数のときは $a_n=k+2$ ， $n-T_k$ が偶数のときは $a_n=k+1$ であると予想できます。これは次の赤字の部分に相当します。

\begin{equation*}
\color{red}{a_n=}
\begin{cases}
\color{red}{k+2} & \color{red}{(k\text{は奇数}, n-T_k\text{は奇数})}\\
\color{red}{k+1} & \color{red}{(k\text{は奇数}, n-T_k\text{は偶数})}\\
k+1 & (k\text{は偶数}, n-T_k\text{は奇数})\\
k+3 & (k\text{は偶数}, n-T_k\text{は偶数})
\end{cases}
\end{equation*}

だんだん分かってきたぞー？

$a_n$ が奇数番目のグループに属するとき

最後に $k$ が偶数かつ $a_n$ が第 $k+1$ 群に属する場合（赤字の値）を考えます。言い換えれば $a_n$ が奇数番目のグループ（第1群以外）に属するときですね。

\begin{array}{llllllllllll}
1, &&&&&&&&&&\\
3, &2, &&&&&&&&&&\\
\color{red}{3}, &\color{red}{5}, &\color{blue}{3}, &&&&&&&&&\\
5, &4, &5, &4, &&&&&&&&\\
\color{red}{5}, &\color{red}{7}, &\color{red}{5}, &\color{red}{7}, &\color{blue}{5}, &&&&&&&\\
7, &6, &7, &6, &7, &6, &&&&&&\\
\color{red}{7}, &\color{red}{9}, &\color{red}{7}, &\color{red}{9}, &\color{red}{7}, &\color{red}{9}, &\color{blue}{7}, &&&&&\\
9, &8, &9, &8, &9, &8, &9, &8, &&&&\\
\color{red}{9}, &\color{red}{11}, &\color{red}{9}, &\color{red}{11}, &\color{red}{9}, &\color{red}{11}, &\color{red}{9}, &\color{red}{11}, &\color{blue}{9}, &&&\\
11, &10, &11, &10, &11, &10, &11, &10, &11, &10, &&\\
\color{red}{11}, &\color{red}{13}, &\color{red}{11}, &\color{red}{13}, &\color{red}{11}, &\color{red}{13}, &\color{red}{11}, &\color{red}{13}, &\color{red}{11}, &\color{red}{13}, &\color{blue}{11}, &\\
13, &12, &13, &12, &13, &12, &13, &12, &13, &12, &13, &12, \\
\color{red}{13}, &\color{red}{15}, &\color{red}{13}, &\color{red}{15}, &\color{red}{13}&&&&&&&
\end{array}

それぞれのグループの奇数番目は最後尾の値と同じで、偶数番目は最後尾の値より2大きいように見えます。最後尾の値は $\color{blue}{k+1}$ で、 $a_n$ は第 $k+1$ 群の $n-T_k$ 番目なので、 $n-T_k$ が奇数のときは $a_n=k+1$ ， $n-T_k$ が偶数のときは $a_n=k+3$ であると予想できます。これは次の赤字の部分に相当します。

\begin{equation*}
\color{red}{a_n=}
\begin{cases}
k+2 & (k\text{は奇数}, n-T_k\text{は奇数})\\
k+1 & (k\text{は奇数}, n-T_k\text{は偶数})\\
\color{red}{k+1} & \color{red}{(k\text{は偶数}, n-T_k\text{は奇数})}\\
\color{red}{k+3} & \color{red}{(k\text{は偶数}, n-T_k\text{は偶数})}
\end{cases}
\end{equation*}

この予想をもとに第13群の残りを埋めるとすると次のようになりますね。

\begin{array}{lllllllllllll}
1, &&&&&&&&&&&\\
3, &2, &&&&&&&&&&&\\
3, &5, &3, &&&&&&&&&&\\
5, &4, &5, &4, &&&&&&&&&\\
5, &7, &5, &7, &5, &&&&&&&&\\
7, &6, &7, &6, &7, &6, &&&&&&&\\
7, &9, &7, &9, &7, &9, &7, &&&&&&\\
9, &8, &9, &8, &9, &8, &9, &8, &&&&&\\
9, &11, &9, &11, &9, &11, &9, &11, &9, &&&&\\
11, &10, &11, &10, &11, &10, &11, &10, &11, &10, &&&\\
11, &13, &11, &13, &11, &13, &11, &13, &11, &13, &11, &&\\
13, &12, &13, &12, &13, &12, &13, &12, &13, &12, &13, &12, &\\
13, &15, &13, &15, &13, &15, &13, &15, &13, &15, &13, &15, &13
\end{array}

あーなるほどね。理解理解。

でもこの予想、場合分けが面倒なだけで証明できそうな気がしません？

ちょっとやってみます。

証明に挑戦

予想の証明に取りかかる前に $a_{22}=a_{24}=a_{26}=a_{28}=7$ ， $a_{23}=a_{25}=a_{27}=9$ の証明を考えてみましょう。 $a_{28}=7$ であること、すなわち
\begin{equation*}
28=1+2+3+4+5+6+7
\end{equation*}という表示が最小であることは明らかです。私はこの式をベースにして“マイナスずらし作戦”を思いつきました。
\begin{alignat*}{2}
22&=&1&+2\color{red}{-}3+4+5+6+7\\
24&=&1&\color{red}{-}2+3+4+5+6+7\\
26&=&\color{red}{-}1&+2+3+4+5+6+7
\end{alignat*}これにより別の数の表示を機械的につくれます。また
\begin{equation*}
\pm1\pm2\pm\cdots\pm 6\le 21 < 22
\end{equation*}であるからこれ以上少ない数では表示できないので $a_{22}=a_{24}=a_{26}=7$ が分かります。

同様にマイナスずらし作戦を利用して

\begin{alignat*}{2}
23&=&1&+2\color{red}{-}3+4+5+6+7\color{red}{-}8+9\\
25&=&1&\color{red}{-}2+3+4+5+6+7\color{red}{-}8+9\\
27&=&\color{red}{-}1&+2+3+4+5+6+7\color{red}{-}8+9
\end{alignat*}

という表示ができます。次は最小性です。9は奇数、8は偶数なので $\pm1\pm2\pm\cdots\pm8$ と $\pm1\pm2\pm\cdots\pm7$ は偶数、つまり23，25，27になりません。そして
\begin{equation*}
\pm1\pm2\pm\cdots\pm 6\le 21 < 23
\end{equation*}なのでこれ以上少なくすることは不可能だと分かります。

あれ？なんか証明の方針が立ってしまったぞ？

ということで、予想の証明に挑戦してみます。

予想

証明
自然数 $n$ に対して， $T_k\le n< T_{k+1}$ となる自然数 $k$ をとる． $n=T_k$ のときは
\begin{equation*}
n=1+2+\cdots +k
\end{equation*}であり， $k=1$ のときは $a_1=1$ ， $k\ge 2$ のときは
\begin{equation*}
\pm1\pm2\pm\cdots\pm(k - 1)\le T_{k - 1}< n
\end{equation*}であるから $a_n=k$ が得られる．

以降， $n\neq T_k$ を仮定する．このとき
\begin{equation*}
\pm1\pm2\pm\cdots\pm k\le T_k < n
\end{equation*}なので $a_n \ge k+1$ までは確定することに注意する．

kが偶数のとき
$k=2k'$ とおく． $n=T_k +2m-1\;(m=1,2,\ldots,k')$ ならば $a_n=k+1$ であることを示す．ここで， $T_k = T_{k+1} - 2k'-1$ なので $m=k'$ のときは $n=T_k +2k' -1 = T_{k+1} - 2$ ．つまり $n=T_k +2m-1$ $(m=1,2,\ldots,k')$ は $T_k< n < T_{k+1}$ のうち $n-T_k$ が奇数であるものをすべて表している．このとき，

\begin{align*}
n&=T_k +2m -1\\
&= T_{k+1} - 2(k'+1-m)\\
&= 1+\cdots\color{red}{-}(k'+1-m)+\cdots+(k+1)
\end{align*}

と表せる（ $1\le k'+1-m\le k'$ ）．よって $a_n=k+1$ が得られる．

次に $n=T_k +2m\;(m=1,2,\ldots,k')$ ならば $a_n=k+3$ であることを示す． $m=k'$ のとき $n=T_k +2k' = T_{k+1} - 1$ であるから $n=T_k +2m$ $(m=1,2,\ldots,k')$ は $T_k< n < T_{k+1}$ のうち $n-T_k$ が偶数である数をすべて表している．このとき，

\begin{align*}
n&=T_k +2m\\
&= T_{k+1} - 2(k'+1-m) +1\\
&= 1+\cdots\color{red}{-}(k'+1-m)+\cdots+(k+1)\color{red}{-}(k+2)+(k+3)
\end{align*}

と表せる（ $1\le k'+1-m\le k'$ ）．ここで， $k+3$ は奇数， $k+2$ は偶数であるから， $n$ と $\pm1\pm2\pm\cdots\pm (k+2)$ および $n$ と $\pm1\pm2\pm\cdots\pm (k+1)$ は偶奇が異なる．したがって $a_n=k+3$ が得られる．

kが奇数のとき
$k=2k'-1$ とおく． $n=T_k +2m$ ならば $a_n=k+1$ であることを示す． $T_k = T_{k+1} - 2k'$ であるから $T_k +2m=T_{k+1} - 2(k'-m)$ となるので， $T_k< n < T_{k+1}$ のうち $n-T_k$ が偶数である数をすべて表すための $m$ の範囲は $1\le m\le k'-1$ である．このとき，

\begin{align*}
n&=T_k +2m\\
&= T_{k+1} - 2(k'-m)\\
&= 1+\cdots\color{red}{-}(k'-m)+\cdots+(k+1)
\end{align*}

と表すことができる（ $1\le k'-m\le k'-1$ ）．よって $a_n=k+1$ が得られる．

最後に $n=T_k +2m-1$ ならば $a_n=k+2$ であることを示す． $T_k< n < T_{k+1}$ のうち $n-T_k$ が奇数である数をすべて表すための $m$ の範囲は $1\le m\le k'$ である．このとき，

\begin{align*}
n&=T_k +2m-1\\
&= T_{k+2}-(k+2)-(k+1)+2m-1\\
&= T_{k+2} - 2(k+2-m)\\
&= 1+2+\cdots\color{red}{-}(k+2-m)+\cdots+(k+2)
\end{align*}

と表すことができる（ $k'+1\le k+2-m\le k+1$ ）． $k+2$ は奇数であるから $n$ と $\pm1\pm2\pm\cdots\pm (k+1)$ は偶奇が異なる．よって $a_n=k+2$ が得られる．

以上より，予想は正しい．■

あとがきと研究課題

OEISに書いてあった謎のConjectureは定理になりました。「予想」と聞くと、めちゃくちゃ難しい問題だと思うじゃないですか。今回の証明は「三角数の漸化式」と「奇数（resp. 偶数）を引くと偶奇が変わる（resp. 変わらない）こと」の知識しか使ってないので、全然難しくないんですよね。誰もやってなかっただけの問題に出会えた私はラッキーだったと思います。これ、OEISのアカウントを作って報告した方がいいのかな？

研究課題は色々残っています。今回は1から連続する自然数の足し引きによって整数をつくりましたが、他の数列でも整数をつくることができるのかについても気になります。例えば、 $(a_n)_n$ を任意の数列として $(b_n)_n$ を
\begin{align*}
b_1 &= a_1,\\
b_2 &= a_1+1,\\
b_3 &= a_2,\\
b_4 &= a_2+1,\\
b_5 &= a_3,\\
b_6 &= a_3+1,\\
\vdots &
\end{align*}のように定義すれば

\begin{align*}
\sum_{k=1}^{2n}(-1)^k b_k &=\underbrace{-b_1+b_2}_{+1}\underbrace{-b_3+b_4}_{+1}-\cdots\underbrace{-b_{2n-1}+b_{2n}}_{+1}\\
&=n
\end{align*}

となるので任意の整数を作れます（負の数は符号を反転させればよいし，0 は $0=-b_1+b_2+b_3-b_4$ によって作れます）。足し引きで1を無限に作れることがポイントなのかもしれません。

また、1番目からN番目の素数の足し引きで整数を作ることができるのかについても気になります。
oeis.org
素数の足し引きなのでゴールドバッハ予想と関係があるか否かは不明ですが、グラフを見るに、数が大きくなるにつれて意外にも規則的に増加しているように見えます。これもk番目までの素数和で区切ることが証明のカギになるんでしょうか？