#今日の推し関数は次の2つの関数です。
f(t)&=\left(\int_{0}^{t}e^{-x^{2}}dx\right)^{2}\\
g(t)&=\int_{0}^{1}\frac{e^{-\left(1+x^{2}\right)t^{2}}}{1+x^{2}}dx
\end{align*}
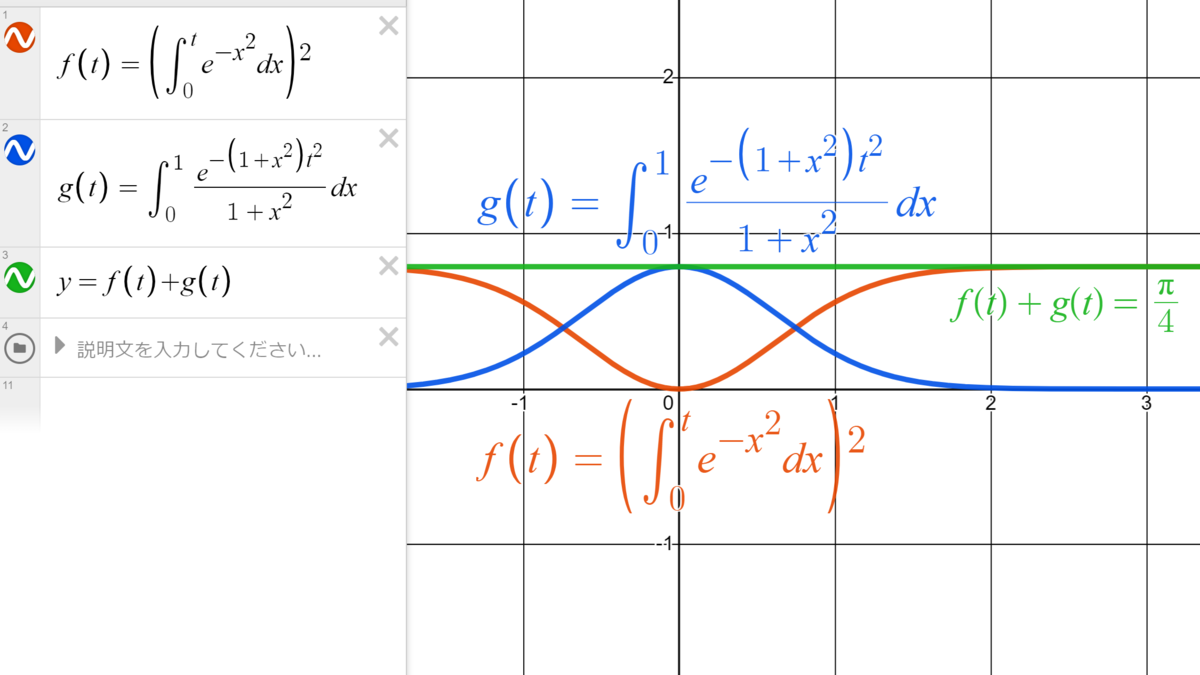
式を見ただけでは「何じゃこれ?」という感じですが、なんと$f+g$は定数関数になります。
\begin{equation}\label{1}
\left(\int_{0}^{t}e^{-x^{2}}dx\right)^{2} + \int_{0}^{1}\frac{e^{-\left(1+x^{2}\right)t^{2}}}{1+x^{2}}dx = \frac{\pi}{4}.
\end{equation}
そして、この等式を使ってガウス積分の半分を計算できるというのが推しポイントです!
厳密なことは忘れて、\eqref{1}において$t\to\infty$とすると、
\[
\left(\int_{0}^{\infty}e^{-x^{2}}dx\right)^{2} + \int_{0}^{1}0\: dx = \frac{\pi}{4}
\]となります。$\int_{0}^{\infty}e^{-x^{2}}dx >0$なので
\[
\int_{0}^{\infty}e^{-x^{2}}dx=\frac{\sqrt{\pi}}{2}
\]がサクッと求まりました。
ラングドシャくらいサクサクでしたね。
では、厳密なことを思い出します。
まず、\eqref{1}が正しいことを確認します。次に、先ほど行った$t\to\infty$としたときの形式的な計算の正当化を見ていきましょう。
命題の証明
まず、$f+g$が定数関数となることを示すために$f'(t)+g'(t)=0$を示します。
\[
f(t)=\left(\int_{0}^{t}e^{-x^{2}}dx\right)^{2}
\]の微分は合成関数の微分と微積分学の基本定理により
\[
f'(t)=2e^{-t^2}\int_0^t e^{-x^2}dx
\]となります。
\[
g(t)=\int_{0}^{1}\frac{e^{-\left(1+x^{2}\right)t^{2}}}{1+x^{2}}dx
\]の微分は、$\varphi(x,t):=\frac{e^{-(1+x^{2})t^{2}}}{1+x^{2}}$とおくと\begin{align*}
g'(t)&=\int_0^1 \frac{\partial}{\partial t}\varphi(x,t)dx\\
&=\int_0^1 -2te^{-\left(1+x^{2}\right)t^{2}}dx\\
&=-2e^{-t^2}\int_0^1 e^{-(tx)^{2}}t\: dx\\
&=-2e^{-t^2}\int_0^t e^{-y^{2}}\: dy\\
&=-f'(t)
\end{align*}となるので、$f+g$は定数関数だと分かりました。
ただし、最初の式変形で
\[
\frac{d}{dt}\int_0^1 \varphi(x,t)dx = \int_0^1 \frac{\partial}{\partial t}\varphi(x,t)dx
\]という微分と積分の順序変更を行いました。これは積分記号下の微分と言われる計算ですが、今回は積分区間が有限なので、偏微分可能性と連続性だけ気にすれば大丈夫です。
正確には、以下の定理を使いました:
\[
\frac{d}{dt}\int_a^b \varphi(x,t)dx = \int_a^b \frac{\partial}{\partial t}\varphi(x,t)dx
\]が成り立つ.
次に、定数関数$f+g$がどんな値をとるのかを決定させるために
\[
f(0)+g(0)=\int_0^1 \frac{1}{1+x^2}dx
\]を計算します。これは$x=\tan\theta$と置換することで
\begin{align*}
\int_0^1 \frac{1}{1+x^2}dx &=\int_0^{\pi/4}\frac{1}{1+\tan^2\theta}\cdot\frac{1}{\cos^2\theta}\: d\theta\\
&=\int_0^{\pi/4} d\theta\\
&=\frac{\pi}{4}
\end{align*}と計算ができますね(あるいは$\tan$の逆関数を用いても計算可能)。これにて\eqref{1}の証明が完了しました。
$t\to\infty$とする
最後に、\eqref{1}の式において$t\to\infty$として
\[
\left(\int_{0}^{\infty}e^{-x^{2}}dx\right)^{2} + \int_{0}^{1}0\: dx = \frac{\pi}{4}
\]と計算してよいことの確認をします。
\[
f(t)=\left(\int_{0}^{t}e^{-x^{2}}dx\right)^{2}
\]に関しては$t\to\infty$としても大丈夫でしょう。強いて言えば$x^2$の連続性
\[
\lim_{t\to\infty}\color{blue}{\left(\color{black}{\int_{0}^{t}e^{-x^{2}}dx}\right)^{2}}=\color{blue}{\left(\color{black}{\lim_{t\to\infty}\int_{0}^{t}e^{-x^{2}}dx}\right)^{2}}
\]を使っていることに注意でしょうか。極限を2乗の中に入れて行っているという意識が無かった方はぜひ気をつけてください。
\[
\lim_{n\to\infty}f(x_n)= f\Big(\lim_{n\to\infty}x_n\Big)=f(a)
\]と書くこともできるため、連続性は極限と関数の順序変更とみることができるのです。
また、細かいことを言うと$\int_{0}^{\infty}e^{-x^{2}}dx$がそもそも存在しないと困るのですが、$t$の関数$\int_{0}^{t}e^{-x^{2}}dx$は単調増加かつ
\begin{align*}
\int_{0}^{t}e^{-x^{2}}dx
&< \int_{0}^{1}e^{-x^{2}}dx + \int_{1}^{\infty}e^{-x}dx \\
&= \int_{0}^{1}e^{-x^{2}}dx + \frac{1}{e}
\end{align*}なので、積分値は確かに存在します。
次に\[
g(t)=\int_{0}^{1}\frac{e^{-\left(1+x^{2}\right)t^{2}}}{1+x^{2}}dx
\]の方ですが、極限と積分の順序変更ができるかどうかのチェックが必要です。つまり
\[
\lim_{t\to\infty}\int_{0}^{1}\varphi(x,t)\: dx=\int_{0}^{1}\lim_{t\to\infty}\varphi(x,t)\: dx
\]としてよい条件をみたす必要があります。
その条件の一つに、次のようなものがあります。
\[
\lim_{n\to\infty}\int_a^b f_n(x)\: dx = \int_a^b f(x)\: dx
\]が成り立つ.
では、$t\to\infty$のとき$\varphi(x,t)=\frac{e^{-(1+x^{2})t^{2}}}{1+x^{2}}$が$0$に一様収束($x$に依存しない収束)することを示します。
$t$を固定したとき、$\varphi(x,t)$は$[0, 1]$で単調減少するので
\[ |\varphi(x,t)|\le\varphi(0,t)=e^{-t^2}\]となります($e^{-t^2}$は$x$に依存しない!)。よって、$t\to\infty$のとき一様に$\varphi(x,t)\to0$となります。ということで、積分と極限の順序変更が可能で、
\begin{align*}
\lim_{t\to\infty}\int_{0}^{1}\frac{e^{-\left(1+x^{2}\right)t^{2}}}{1+x^{2}}dx
&= \int_{0}^{1}0\: dx \\
&= 0
\end{align*}が成り立ちます。
ラングドシャのサクサク感について
ということで
\[
\left(\int_{0}^{t}e^{-x^{2}}dx\right)^{2} + \int_{0}^{1}\frac{e^{-\left(1+x^{2}\right)t^{2}}}{1+x^{2}}dx = \frac{\pi}{4}
\]という等式において、形式的に$t\to\infty$としてよいことが確認できました。
この後のガウス積分の計算を「ラングドシャと同じくらいサクサク」と表現しましたが、計算のサクサク感とお菓子のサクサク感は数学的に未定義です(多分)。
つまり、「ラングドシャと同じくらいサクサク」という主張は数学的な主張ではなく、比喩表現に過ぎません。
…ここの厳密性いらないな?