三目並べ(○×ゲーム,まるぺけ,tic-tac-toe)とは、3×3のマスを用意し、先手と後手がそれぞれ「○」と「×」を交互に書き込んでいき、縦横ナナメのどれか3個を並べた方が勝ちというゲームです。
紙とペンがあれば友達と手軽に楽しめます。お一人様でもGoogleで「三目並べ」「tic-tac-toe」と検索すればPC対戦ができます。三目並べ経験者ならご存知かと思いますが、凡ミスをしなければ引き分けになります。実際、三目並べは先手・後手ともに最善手であれば必ず引き分けであることが知られています。
mathtrain.jp
これでは少々つまらないので、ルールを少し変えて
三目並べをトーラスやクラインの壺にしてみる
というのはどうでしょう?
PC上でもスマホアプリでも遊ぶことができます。「三目並べ」の他にも、「五目並べ」「迷路」「クロスワード・パズル」「ことば探し」「ジグソー・パズル」「チェス」「ビリヤード」「マインスイーパ」が遊べます(太字が私のおすすめ)。
「トーラス」と「クラインの壺」の基本的なこと
2次元トーラス(Torus)とはドーナツの表面を表す曲面のことです。
クラインの壺(Klein bottle)はトーラスとほんの少し似ています(?)が、表裏のない(向き付け不可能な)所が特徴的な曲面です*1。
今日やりたいことは3×3のマスをトーラスやクラインの壺に変形して三目並べをすることです。実際に作ってみましょう。

…と思ったけど図描くのむずくね?○×書きにくくね?きれいに描けなかったので諦めましたごめんなさい(描けたらこっそり載せるかも)。そもそも紙・黒板・曇った窓ガラス等で手軽に遊べるのがウリのゲームで毎回複雑な図を描くのは面倒くさいですよね。
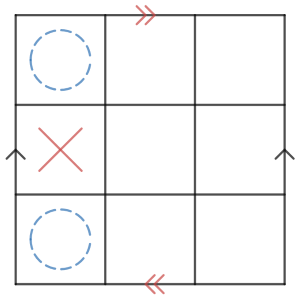
そこで、代わりに変形前の図でやりましょう。

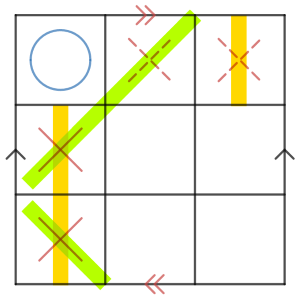
これならお手軽!それぞれ2種類の矢印がありますが「対辺を矢印の向きを揃えて同一視してください」という意味です。「四角形をぐにゃっと曲げて辺を貼り合わせてもよい」と思って構いません。実際に対辺を向きを揃えて貼り合わせるとトーラス及びクラインの壺を作ることができます。このように、複雑な図形を四角形などの基本的な図形に変形・分解する操作は位相幾何などではよくやります。
大まかな解説が終わったので、次章からいよいよ実戦です。
\begin{align*}
&(x_1,y_1)\sim(x_2,y_2)\\
\overset{def.}{\iff}&(x_1,y_1)=\begin{cases}(x_2,y_2)\\
(x_2\pm1,y_2)\\
(x_2,y_2\pm1)\\
(x_2\pm1,y_2\pm1)\end{cases}
\end{align*}を入れたときの商空間
同様にして、クラインの壺は次の同値関係を用いて定義できます:
\begin{align*}
&(x_1,y_1)\sim(x_2,y_2)\\
\overset{def.}{\iff}&(x_1,y_1)=\begin{cases}(x_2,y_2)\\
(x_2\pm1,y_2)\\
(1-x_2,y_2\pm1)\\
(1-x_2\pm1,y_2\pm1)\end{cases}
\end{align*}
トーラス上の三目並べ
それでは実際にトーラス上で三目並べをやってみましょう。×が私です。
あ。負けた。左右(および上下)の辺は同一視しているため、トーラスならではの勝ちパターンがあるのが面白いですね。
今度は本気でやります。
はい勝ち~~~!本気出せば余裕だし!*2
……すみませんちょっと調子に乗っちゃいました。というのも以前からこのゲームを嗜んできた私ですから、誰だろうと絶対勝ててしまうのです。自作自演なんじゃないの?と思ったそこのあなた、何なら300円賭けてもいいですよ。あ、その代わり先手は私からでいいですか?お願いします300円あげるので先手は私からで…はいありがとうございます…
そうなんです、実はトーラス上で三目並べをするときは先手必勝(五手詰*3)なのです!
先手必勝であることの解説
まず、ふつうの三目並べの場合、隅・辺・中央の3通りあります。
\begin{array}{c|c|c}
\text{隅}&\text{横}&\text{隅}\\
\hline \text{横}&\text{中}&\text{横}\\
\hline \text{隅}&\text{横}&\text{隅}
\end{array}ところが、トーラス上で三目並べをするときは場合分けはありません。隅や辺などは無く、どこに打っても本質的に同じ手だからです!
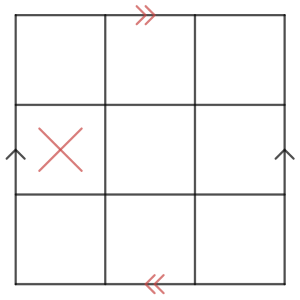
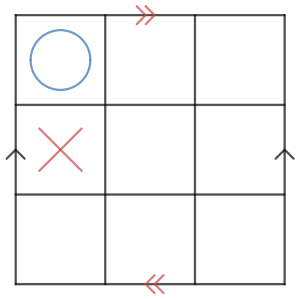
ということで、先手は中央に打つことにします。

後手の打ち方は×の斜めと横の2通りです。しかし、×の横に打つ手は通常の三目並べでも悪手*4なので斜めのときを考えましょう。

先手の番です。(実はどこでもいいのですが)例えばここに打ってみましょう。
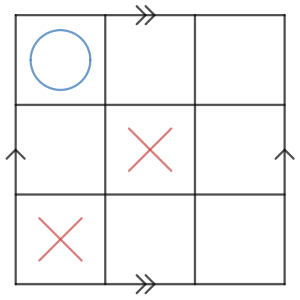
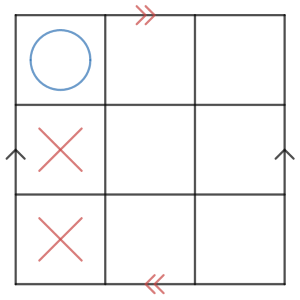
このとき、後手は斜めの列が揃うのを阻止するのが最善です。

さりげなく後手がリーチなので、先手も負けじと阻止します。
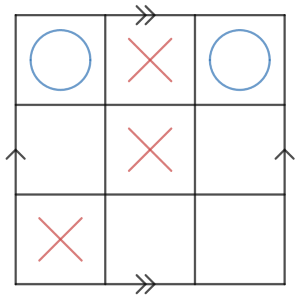
…あっ
皆さんお気づきでしょうか。実はこの時点でダブルリーチになっています。
対戦例もお見せしたので簡単ですかね…?
よろしければ考えてみてください!
そろそろ正解、いきます!
正解
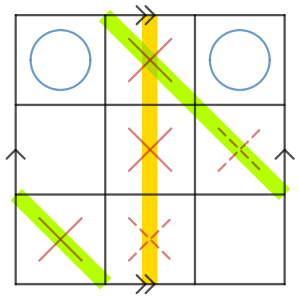
はい、このようなダブルリーチがありますね。よって、トーラス上の三目並べは先手必勝(五手詰)であることが分かりました。
クラインの壺上の三目並べ
今度はクラインの壺での三目並べです。×が私です。
クラインの壺だとこんなのもアリなんです!超たのしい!
ピンと来ない方もいるかもしれませんが、斜めの列は「左+上」のように追うと分かりやすいです。また、紙上での対人戦では揃った列に気付かないまま続行もあり得るのでお気をつけください。
さて、クラインの壺でも先手必勝が予想されますが、トーラスのときよりも早く勝てたような気がしませんか…?
なんと、クラインの壺でも先手必勝で、しかも三手詰なのです!
先手必勝であることの解説
トーラスの場合は隅も辺もないため、どこに打っても本質的に変わりませんでした。クラインの壺でも同じかと思いきや、2種類あります。
このように、両サイドに打つ手はリーチを上下に伸ばすことができます。これがトーラスとの大きな違いです。したがって、両サイドに打つ手は本質的に同じです。そして、残っている中央縦ラインはすぐに自分の所へ帰ってしまうので状況が異なります。この2パターンに分けて考えます。
①先手が両サイドに打つ時
先手はここに打つことにします。
このとき、後手の打つべき手は次の2通りでしょう。
なぜなら、後手がこれら以外の手を打つと、先手は両端に止まりのない連続した2個の×を作れるため勝ちが確定します。
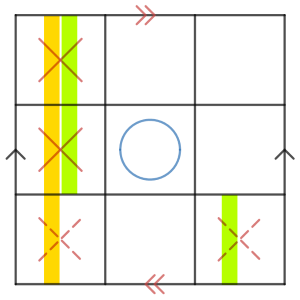
そこで、後手はここを選ぶことにしましょう。
実はこの場合でも、先手はダブルリーチを作れるので勝ててしまいます。さて、その一手とはどこでしょうか?(解は複数あります)
よろしければ考えてみてください!
正解、行きますよ?
解答例
クラインの壺、やばい。
別解は次の通りです:\begin{equation*}
\begin{array}{c|c|c}
\circ&\color{red}{\times}&\:\:\:\\
\hline \times&&\\
\hline &&\end{array}\quad
\begin{array}{c|c|c}
\circ&\:\:\:&\color{red}{\times}\\
\hline \times&&\\
\hline &&\end{array}
\end{equation*}どこがダブルリーチになっているのかについては皆さまに任せたいと思います。
②先手が中央縦ラインに打つ時
上下にリーチを伸ばせないので悪い手に見えますが…これでも勝てます!こちらのパターンでの必勝法は最初の対戦例がヒントになっていますので割愛します。個人的にこちら側の手の方がアクロバティックで好き。
まとめ
三目並べをトーラスやクラインの壺にすることで一味違う楽しみ方ができましたね。ぜひ必勝法を知らない友達と一緒に遊んでみてください。
最後に、投稿直前の思いつきなのですが、別ルール「お互いに×を書き込んでいき、列を揃えたほうが負け」も面白そうです。えーっと、この場合の必勝法は……私が全部答えを書いてしまうのはつまらないですよね。詳しい考察は皆さんにお任せして記事を終わりにしたいと思います。
何か質問等があれば下のコメントでお願いします!
thank Q for rEaDing.φ(・▽・ )