Corollaryは必然に。

日本では政治のみならず、多くの業界で「総選挙」が行われていますね。私は投票するほど興味はないんですけど、結果だけはつい知りたくなってしまいます。そこでふと思ったんですけど、

「自然数が選ぶ自然数総選挙」

を行ったら、どんな結果が起こりえるでしょうか？自然数みずから自分の順位を決める投票をするのは少し変ですが、『若手声優が選ぶ声優総選挙』という特番もあったので、いいんじゃないでしょうか？

まずはルールの設定から

ルール

有権者は自然数の皆さま。つまり、「1さん」「2さん」「3さん」…「5000兆さん」…と無限にいる*1。
投票する先も自然数の皆さま。また、自分に投票してもよい。
一人一票で、複数票・白票はないものとする。

ここで記号を導入します。 $f(n)$ を自然数 $n$ さんの投票先を表すことにします。例えば、\begin{equation*}f(1)=3\end{equation*}ならば、「1さんは3さんに投票」を表します。これで「自然数が選ぶ自然数総選挙」は「自然数全体から自然数への関数（数列）」で表せるようになりました。やったー！

それでは、「自然数が選ぶ自然数総選挙」をしたら何が起きるのか？面白そうなものを簡単に紹介します。

全員に1票ずつ

平和な結果（？）です。これは自然数全員が自分自身に投票すれば起こり得ますね。つまり、\begin{equation*}f(n)=n\end{equation*}と投票すればよいです。今のはつまらない投票ですが、ちょっと手を加えて
\begin{equation*}f(n)=n+(-1)^{n+1}\end{equation*}という投票だったとしても全員1票ずつ入ります。試しに計算してみると分かりますが、
\begin{align*}
f(1)=2,\qquad& f(2)=1,\\
f(3)=4,\qquad& f(4)=3,\\
f(5)=6,\qquad& f(6)=5,\ldots
\end{align*}といった具合に投票されています。一つの結果に対して、投票方法は一通りとは限らないので気をつけてください。

一人だけ0票、他1票

無限に投票者がいるのに、誰にも投票されなかった人、つらそう。これは例えば\begin{equation*}f(n)=n+1\end{equation*}という投票を考えると、1さんが0票、他は1票入ります。特に意味は無いですが例えば20さんが0票になるパターンは
\begin{equation*}f(n)=\begin{cases}
n & (n<20)\\
n+1 & (n\geqq20)
\end{cases}\end{equation*}などがあります。

一人だけ無限票、他0票

†圧倒的勝利†

これは例えば全員が1さんに投票したときに起こります。つまり、\begin{equation*}f(n)=1\end{equation*}です。特に意味は無いですが例えば20さんを無限票にしたいなら\begin{equation*}f(n)=20\end{equation*}でよいでしょう。

全員に「2票」ずつ

平和な結果（？）パート2です。しかし、今度は全員に2票入ります！この辺りから有権者が無限人ならではの現象が垣間見ることができます。
\begin{equation*}f(n)=\begin{cases}
\frac{n+1}{2} & (n\text{は奇数のとき})\\
\frac{n}{2} & (n\text{は偶数のとき})
\end{cases}\end{equation*}という投票を考えてみましょう。 $f(n)=\operatorname{ceil}(\frac{n}{2})$ としても構いません*2。実際に計算すると
\begin{align*}
f(1)=1,\qquad& f(2)=1,\\
f(3)=2,\qquad& f(4)=2,\\
f(5)=3,\qquad& f(6)=3,\ldots
\end{align*}となります。「1さんは、1自身と2さんの2票」「2さんは、3さんと4さんの2票」「3さんは、5さんと6さんの2票」であることが分かります。要するに、「 $n$ さんに投票するのは $2n-1$ さんと $2n$ さんの2票」であるようにしました。ちなみに、5000兆さんには9999兆9999億9999万9999さんと1京さんが投票してくれます。これで全員に丁度2票入ることが分かりました。

少し一般化して、全員に $k$ 票ずつ入るようにするにはどうすればいいでしょうか？場合分けで定義することもできますが、ceilを使えば $f(n)=\operatorname{ceil}(\frac{n}{k})$ とすればいいですね。 $f(n)=\operatorname{ceil}(\frac{n}{5000\text{兆}})$ とすれば、全員に5000兆票入ります！わあ、私も5000兆票欲しい！

1位が存在しない

徳光「自然数が選ぶ自然数総選挙、第1位ッ………！いません！」

立候補者が無限なのでこういうこともあります。つまり、獲得票数の最大値が存在しないパターンです。ひとまず次の例をご覧ください。

まず、自然数たちを次のようにグループ分けします:

\begin{equation*}
1\color{red}{\mid} 2,3\color{red}{\mid} 4,5,6\color{red}{\mid} 7,8,9,10\color{red}{\mid} 11,12,13,14,15\color{red}{\mid} 16,\ldots
\end{equation*}

第1群は1人、第2群は2人、第3群は3人、…、第 $n$ 群は $n$ 人になるように分けました。そして、第1群は1さんに、第2群は2さんに、第3群は3さんに、…、第 $n$ 群は $n$ さんに投票させましょう。
\begin{align*}
f(1)&=1\\
f(2)=f(3)&=2\\
f(4)=f(5)=f(6)&=3\\
f(7)=f(8)=f(9)=f(10)&=4\\
&\vdots
\end{align*}といった感じです。1さんは1票、2さんは2票、3さんは3票獲得しています。5000兆さんは

\begin{equation*}
\frac{(5000\text{兆}-1)5000\text{兆}}{2} < m \leqq \frac{5000\text{兆}(5000\text{兆}+1)}{2}
\end{equation*}

を満たす5000兆人の自然数 $m$ さんたちが投票してくれます。さて、このときの1位は誰でしょうか？最も多く獲得した人は誰でしょうか？上には上が「無限に」いるので、1位はいませんね。

補足　「…」を用いずに，閉じた式で $f$ を表現します． $f(n)$ の値は $\frac{(k-1)k}{2}< n\leqq \frac{k(k+1)}{2}$ を満たす唯一の自然数 $k$ を用いて $f(n)=k$ と表せます．この $k$ を $n$ の式で表すことが目標です．2つの不等式 $\frac{(k-1)k}{2}< n,\quad n\leqq \frac{k(k+1)}{2}$ を $k$ について解いて一つにまとめると， $\frac{-1+\sqrt{1+8n}}{2}\leqq k<\frac{1+\sqrt{1+8n}}{2}=\frac{-1+\sqrt{1+8n}}{2}+1$ となります．したがって，これを満たす自然数 $k$ は\begin{equation*}k=\operatorname{ceil}\left(\frac{-1+\sqrt{1+8n}}{2}\right)\end{equation*}と表せます．つまり， $f(n)=\operatorname{ceil}\left(\frac{-1+\sqrt{1+8n}}{2}\right)$ が得られました．試しに $n=1$ から代入すれば\begin{equation*}1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5,\ldots \end{equation*}となっていることが分かると思います．

全員に「無限票」ずつ

無限人の立候補者が無限票獲得…平和な結果ですね（震え声）。こんな不思議な現象も確かに起きるのです。早速、全員に無限票入るように有権者を誘導します。

先ほどと同じように、自然数たちをグループ分けします:

\begin{equation*}
1\color{red}{\mid} 2,3\color{red}{\mid} 4,5,6\color{red}{\mid} 7,8,9,10\color{red}{\mid} 11,12,13,14,15\color{red}{\mid} 16,\ldots
\end{equation*}

そして、そのグループの中で小さい順に番号づけしたときの数の人に投票するように仕向けます。投票先を矢印で表すとこうなります:

\begin{array}{c|cc|ccc|cccc|ccccc|l}
1 &2, &3 &4, &5, &6 &7, &8, &9, &10 &11, &12, &13, &14, &15 &16,\ldots\\
\downarrow & \downarrow & \downarrow & \downarrow &\downarrow &\downarrow & \downarrow &\downarrow &\downarrow &\downarrow & \downarrow &\downarrow &\downarrow &\downarrow &\downarrow & \downarrow\\
1 &1, &2 &1, &2, &3 &1, &2, &3, &4 &1, &2, &3, &4, &5 &1,\ldots
\end{array}

開票されていく様子を図にしてみました:
f:id:corollary2525:20170621232905g:plain

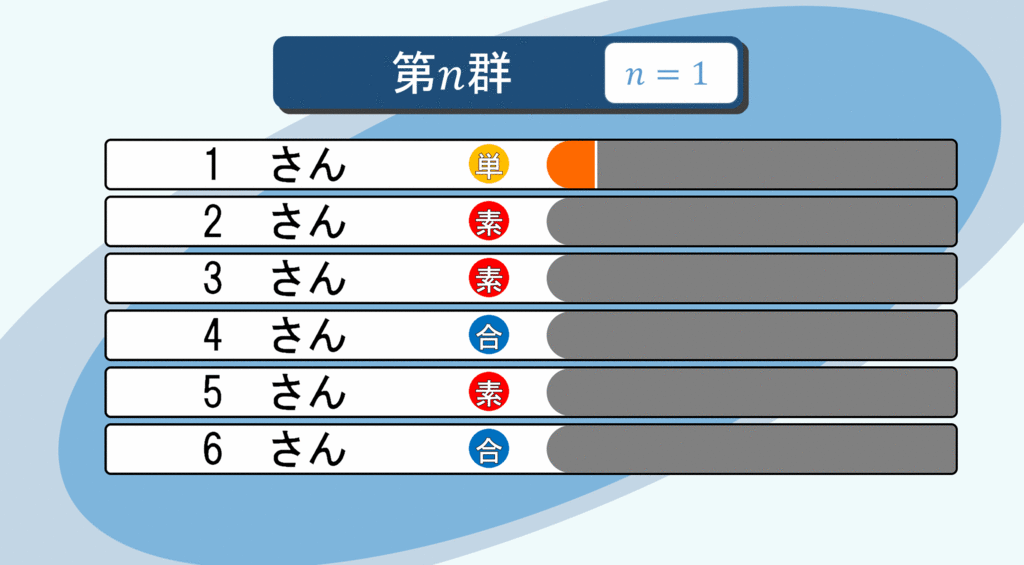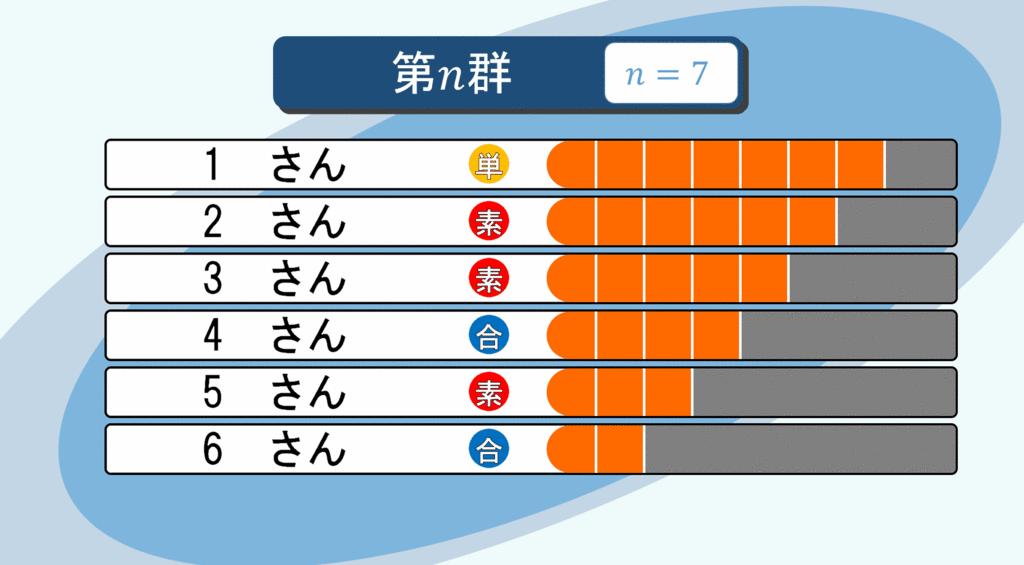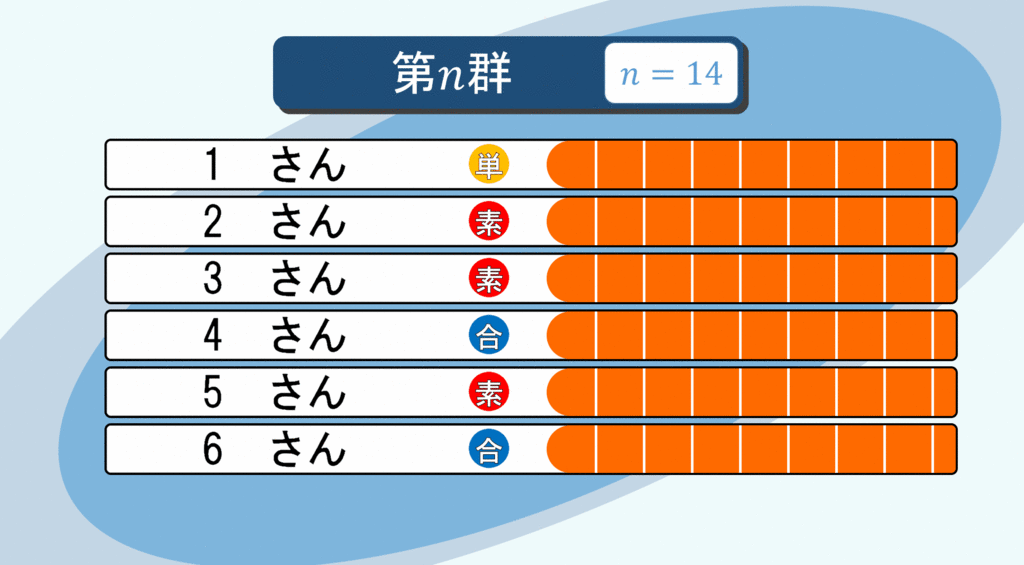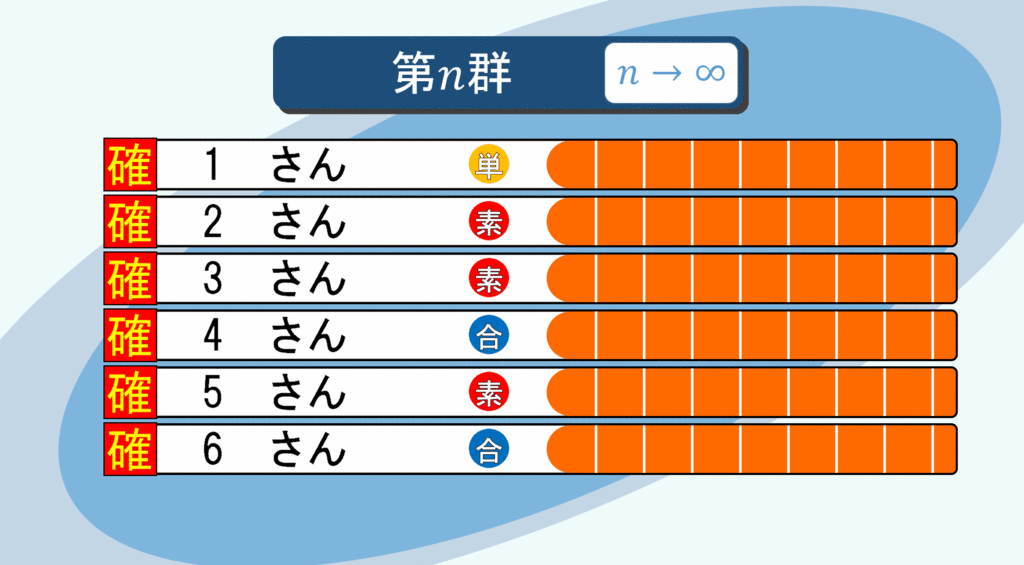
有限で止めれば1さんが多く票を集めることになります。しかし、無限に続ければ、どんなに巨大な自然数さんもいずれ投票してくれる人が「無限に」現れます。

補足　この $f$ も閉じた式で表したいと思います．各 $n$ に対して， $\frac{(k-1)k}{2}< n\leqq \frac{k(k+1)}{2}$ を満たす自然数は $k=\operatorname{ceil}\left(\frac{-1+\sqrt{1+8n}}{2}\right)$ と表せました．この $k$ を $k_n$ と書き改めることにすると，\begin{equation*}f(n)=n-\frac{(k_n-1)k_n}{2}\end{equation*}と定義すればおしまいです．試しに $n=1$ から代入すれば\begin{equation*}1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1,\ldots \end{equation*}となっていることが分かると思います．

一人だけ0票、他無限票

†圧倒的敗北†

1さんだけ0票にしたいならば、先ほどの投票先にすべて1を足せばよいですね。

\begin{array}{c|cc|ccc|cccc|ccccc|l}
1 &2, &3 &4, &5, &6 &7, &8, &9, &10 &11, &12, &13, &14, &15 &16,\ldots\\
\downarrow & \downarrow & \downarrow & \downarrow &\downarrow &\downarrow & \downarrow &\downarrow &\downarrow &\downarrow & \downarrow &\downarrow &\downarrow &\downarrow &\downarrow & \downarrow\\
2 &2, &3 &2, &3, &4 &2, &3, &4, &5 &2, &3, &4, &5, &6 &2,\ldots
\end{array}

あるいは、1さんに投票している人を2さんに変更してもいいですね。

\begin{array}{c|cc|ccc|cccc|ccccc|l}
1 &2, &3 &4, &5, &6 &7, &8, &9, &10 &11, &12, &13, &14, &15 &16,\ldots\\
\downarrow & \downarrow & \downarrow & \downarrow &\downarrow &\downarrow & \downarrow &\downarrow &\downarrow &\downarrow & \downarrow &\downarrow &\downarrow &\downarrow &\downarrow & \downarrow\\
\color{red}{2} &\color{red}{2}, &2 &\color{red}{2}, &2, &3 &\color{red}{2}, &2, &3, &4 &\color{red}{2}, &2, &3, &4, &5 &\color{red}{2},\ldots
\end{array}

今紹介した方法を応用すれば、任意の $m$ さんを0票、他の人を無限票にできます。そうです、 $m$ さんに入っている票を $m+1$ さんの票に変更すればいいんです。ひどい不正です。

補足　ちゃんと式で表してみましょう．各 $n$ に対して， $k_n=\operatorname{ceil}\left(\frac{-1+\sqrt{1+8n}}{2}\right)$ とおき，\begin{equation*}f(n)=n-\frac{(k_n-1)k_n}{2}\end{equation*}と定義すれば\begin{equation*}1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1,\ldots \end{equation*}という数列を表すことは前節で説明しました．そこで， $m$ を固定し，\begin{equation*}f_m(n)=f(n)+\delta_{m,f(n)}\end{equation*}というのを考えます．ただし， $\delta_{i,j}$ はクロネッカーのデルタを表します:
\begin{equation*}\delta_{i,j}=
\begin{cases}
1&(i=j)\\
0&(i\neq j)
\end{cases}.\end{equation*} $\delta_{m,f(n)}$ の部分は基本的に0ですが， $f(n)=m$ のときにだけ $\delta_{m,f(n)}=1$ になります．つまり，書き換えると\begin{equation*}f_m(n)=\begin{cases}
m+1&(f(n)=m)\\
f(n)&(f(n)\neq m)
\end{cases}\end{equation*}となります．したがって， $n$ に何を代入しても $f_{m}(n)\neq m$ であること，すなわち $m$ さんが0票であることが分かります．