Corollaryは必然に。

最近、メタモンがピカチュウにへんしんする様子を数式で表しました。

メタモンのへんしん！https://t.co/hNaGFHTW9b @Desmos pic.twitter.com/I9Mls3ZNdA
— コロちゃんぬ (@corollary2525) 2016年9月25日

【追記】次のように改良しました。
メタモンのへんしん！ver1.1 #desmos https://t.co/uI374ZH3n7 pic.twitter.com/10iC3C9l7j
— コロちゃんぬ (@corollary2525) 2016年11月23日

これがなかなか好評だったので、今回は「メタモンのつくり方」を解説したいと思います（へんしん方法は気が向いたら書きます）。

※数式お絵描きをする際は、グラフ作成ソフトが必要です。私はブラウザアプリ「Desmos」をよく利用します。今回はこれを使って説明します。他にも「GeoGebra」「GRAPES」などといった数学ソフトウェアが有名です。お好きなものをどうぞ。

グラフのかき方

グラフのかき方は大きく分けて2通りあります。1つ目は
\[
y=2x+1,　x^2+y^2=9
\]などといった $x$ と $y$ の条件を書く方法です。2つ目は
\[
(t,2t+1),　(3\cos t, 3\sin t)
\]のように媒介変数を利用した方法です。どちらを使うかは描く絵によって使い分けましょう。

メタモンは滑らかな閉じた曲線なので、媒介変数表示でお絵描きしたいと思います。

準備1: 円で土台作り

まずは、メタモンの画像を重ねて、円で土台を作ります。

f:id:corollary2525:20161003235742p:plain

この円は次のように書きました。

\[
(\sqrt{14}\cos t, \sqrt{14}\sin t)
\]

$\sqrt{14}$ は円の半径です（画像を大きくすれば半径4でもできたのに…センスないですね）。

また、 $t$ の範囲は $0\le t\le 2\pi$ が一般的ですが、 $-\pi\le t\le \pi$ のほうが数の絶対値が小さいので扱いやすいと思います。

準備2: 軟化子(に利用される関数)

あとはこの円にメタモン特有の「滑らかな出っ張り」を加えることができれば描けそうです。「滑らかな出っ張り」を表現するのに使ったのがこちらの関数です。

\[
m(x)=
\begin{cases}
e^{-\frac{1}{1-x^2}} & |x|< 1\\
0 & |x|\ge 1
\end{cases}\] f:id:corollary2525:20161004001240p:plain

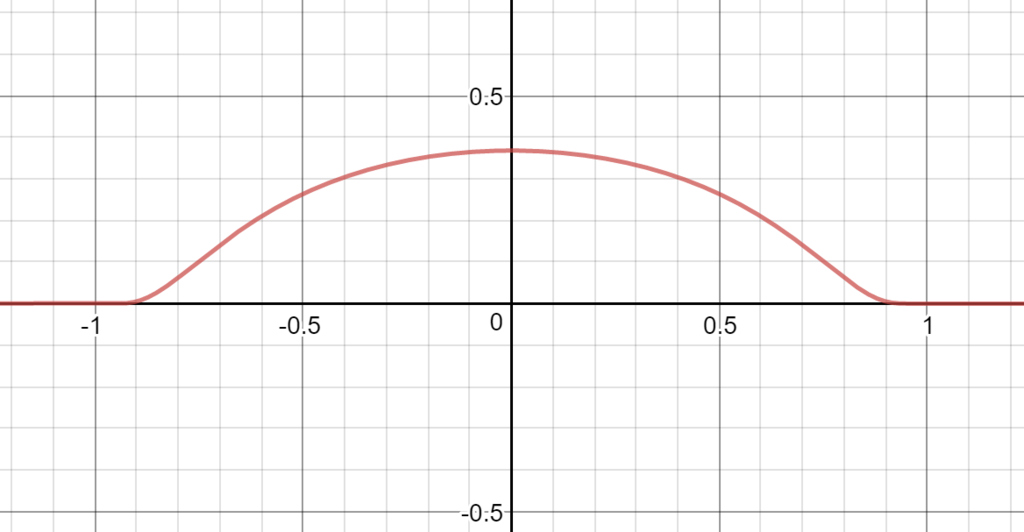
数学では「軟化子(mollifier)」「カットオフ関数」として利用される関数です。この関数の特徴は次の2つです。

$-1\le x\le 1$ の外側での値は0
境目( $x=\pm1$ )も含め、すべての点で無限回微分可能

1つ目の性質のおかげで要所要所に $m(x)$ を加えても他の場所に影響がありません。また、2つ目の性質で滑らかさを表現できるので、メタモンのお絵描きに最適です。

準備ができたので、いよいよお絵描きしていきます。

STEP1: $m(x)$ を円の $x$ 成分に追加してみる

最初に $m(x)$ を定義します。Desmosであれば以下のように書いておきます。
f:id:corollary2525:20161004012418p:plain

さて、土台の円 $(\sqrt{14}\cos t, \sqrt{14}\sin t)$ の $x$ 成分に $m(t)$ を足してみましょう。
f:id:corollary2525:20161004014211p:plain

この曲線は、円の $t=0$ 付近に「 $x$ 軸方向の山」が加わったことを意味するので、このような曲線になることが理解いただけるでしょうか。
f:id:corollary2525:20161004014220p:plain

STEP2: 横幅の調節

横幅が広すぎるので調節します。横幅を1/2にしたければ、 $m(2t)$ とすればOKです。今回は2.2にしました。
f:id:corollary2525:20161004015528p:plain

STEP3: 高さの調節

高さが3倍くらいほしいので、そういうときは $3m(t)$ としましょう。STEP2の変形と合わせて $3m(2.2t)$ となりました。
f:id:corollary2525:20161004021607p:plain

いい感じです。

STEP4: 移動

メタモンの左手の所まで移動させます。およそ $\frac{\pi}{10}$ (度数法だと $18^{\circ}$ )の位置にあるので、そこまで移動させたいときは $t$ を $t-\frac{\pi}{10}$ に置き換えます。つまり、 $m(t-\frac{\pi}{10})$ と書けばよいのです。ちょっとこだわって $m(t-\frac{1.1\pi}{10})$ にしました。STEP3までの調節と組み合わせて
\[
3m\bigg(2.2\Big(t-\frac{1.1\pi}{10}\Big)\bigg)
\]となりました。
f:id:corollary2525:20161004023220p:plain

これで「メタモンの左手の『 $x$ 成分』」が終了です。

STEP5: $y$ 成分

『 $y$ 成分』にも同じような式を加えていくのです。試行錯誤して
\[
2m\left(2.2\left(t-\frac{1.1\pi }{10}\right)\right)
\]を $y$ 成分に加えることにしました。 $m$ の括弧の中（横幅と移動）は $x$ 成分と同じでよいので、高さだけ調節すれば良いでしょう。
f:id:corollary2525:20161004030556p:plain

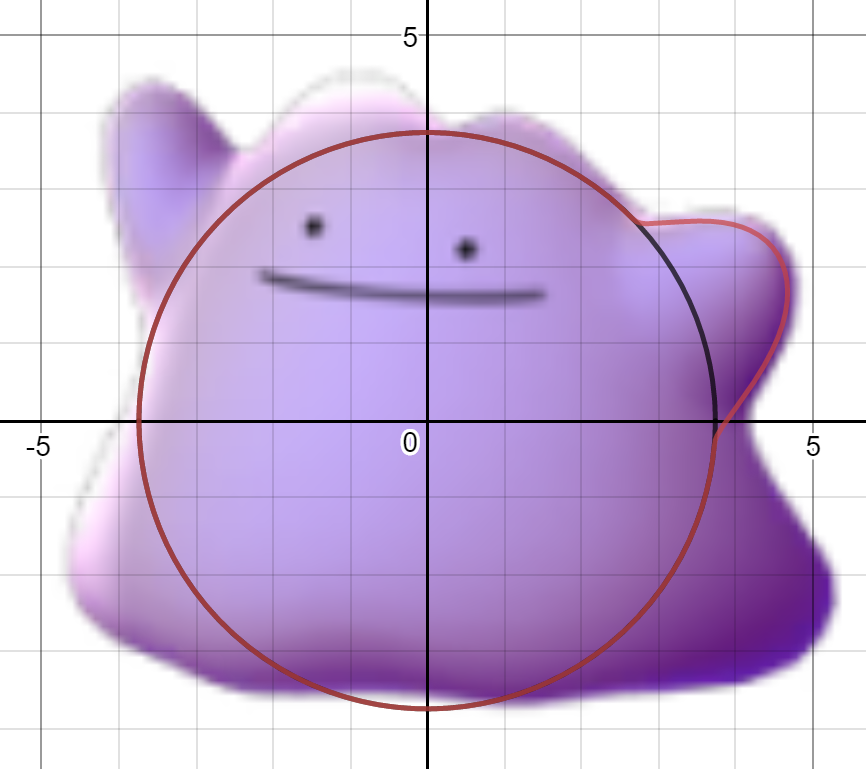
これで「メタモンの左手」の完成です！この作業の繰り返しによってメタモン曲線はできています。ただし、このまま書き続けると長すぎて書ききれなくなってしまうので、
\[
(f_1(t)+f_2(t),g_1(t)+g_2(t))
\]のようにいくつかのパートに分けてあげると良いと思います。ちなみに私は $f_1(t), g_1(t)$ を上半身パート、 $f_2(t), g_2(t)$ を下半身パートに分けました。